Rangkuman Materi Relasi dan Fungsi Kelas 10
Ini adalah rangkuman materi relasi dan fungsi kelas 10 SMA yang mencakup mulai dari konsep dasar teori sampai kumpulan soal relasi dan fungsi beserta pembahasannya lengkap.
Relasi dan fungsi adalah dua hal yang yang berbeda dalam matematika.
Suatu relasi bisa jadi merupakan suatu fungsi namun demikian suatu fungsi pasti adalah sebuah relasi.
Yup, kamu ngga salah dengar.
Antara relasi dan fungsi mempunyai hubungan satu sama lain.
Relasi lebih bersifat umum, sedangkan suatu fungsi lebih eksklusif dengan aturan yang lebih spesifik jika dibandingkan dengan konsep relasi.
Pengertian Relasi dan Fungsi
Relasi merupakan hubungan dua buah himpunan yang bersifat umum, tidak ada aturan spesifik yang mengatur keduanya.
Untuk lebih jelasnya kamu bisa melihat suatu relasi "faktor dari" yang dinyatakan dalam bentuk diagram venn berikut ini.
Terlihat jelas dalam diagram venn tersebut jika bilangan 1 anggota himpunan $A$ bebas dipasangkan dengan kelima bilangan anggota himpunan $B$ karena angka satu merupakan faktor dari semua bilangan.
Demikian juga bilangan 2 anggota himpunan $A$ dia juga dipasangkan pada empat anggota himpunan $B$.
Kondisi tersebut akan berbeda jauh jika hubungan dua himpunan $A$ dan himpunan $B$ dinyatakan oleh sebuah fungsi.
Secara matematis fungsi adalah sebuah aturan tertentu yang memasangkan setiap anggota himpunan $A$ tepat satu pada anggota himpunan $B$.
Pada sebuah fungsi hubungan antara anggota himpunan $A$ dan anggota himpunan $B$ sudah diatur lebih spesifik lagi dengan ketentuan bahwa setiap anggota himpunan $A$ harus habis dipasangkan dengan hanya satu pasang anggota $B$.
Artinya adalah bahwa pada masing - masing atau setiap anggota himpunan $A$ tidak ada yang boleh dobel atau pun bercabang lebih untuk dipasangkan dengan anggota himpunan $B$.
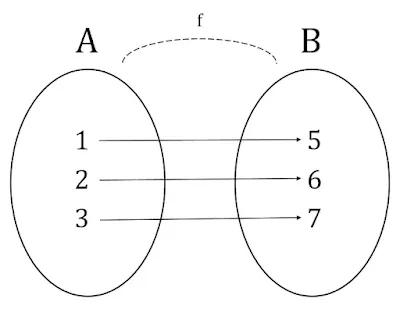
Sebagai gambaran lebih jelas kamu bisa perhatikan gambar diagram venn di bawah ini yang menggambarkan suatu fungsi $f(x)=x+1$.
Terlihat jelas bukan perbedaan keduanya diantara relasi dan fungsi.
Pada sebuah fungsi bukan jadi persoalan jika ada anggota himpunan $B$ lebih dari satu dipasangkan dengan satu, dua atau lebih anggota himpunan $A$.
Bahkan jika ada yang sama sekali tidak dipasangkan dengan anggota himpunan $A$.
Seperti terlihat bahwa bilangan $5$ dan $6$ sama sekali tidak mempunyai pasangan dengan anggota himpunan $A$.
Domain, Kodomain dan Range Fungsi
Jika kita cermati lagi diagram venn dari fungsi $f(x)=x+1$ di atas maka kita akan dapatkan 3 hal yang penting, yaitu :
- $A=\big \{ 1,2,3 \big \}$
- $B=\big \{ 2,3,4,5,6 \big \}$
- Hasil yang dipasangkan $=\big \{ 2,3,4 \big \}$
Nah, selanjutnya $A=\big \{ 1,2,3 \big \}$ disebut juga dengan domain (daerah asal), sedangkan $B=\big \{ 2,3,4,5,6 \big \}$ akan disebut dengan kodomain (daerah kawan).
Sedangkan $\big \{ 2,3,4 \big \}$ akan disebut dengan range (daerah hasil) dari fungsi $f(x)=x+1$ tersebut.
Pengertian lebih jauh jika kita pahami, sebuah domain akan lebih berperan terhadap syarat sebuah fungsi agar terdefinisi pada himpunan bilangan Real ($x \in \Re$).
Sedangkan range merupakan batas - batas dari nilai hasil dari sebuah fungsi itu sendiri.
Jika $f(x)$ adalah sebuah fungsi yang terdefinisi untuk setiap $x$ elemen atau anggota himpunan bilangan Real maka :
- $f(x)=\sqrt{ax+b}$ maka $D_f=\big \{ x \ \big| \ ax+b \ge 0,x \in \Re \big \}$.
- $f(x)=\dfrac{ax+b}{cx+d}$ maka $D_f=\big \{ x \ \big| \ cx+d \ne 0,x \in \Re \big \}$.
Jenis - Jenis Fungsi Kamu Wajib Tahu
Di bawah ini adalah beberapa jenis fungsi yang wajib untuk kamu tahu, diantaranya yaitu :
1. Fungsi Konstan
Sebuah fungsi dikatakan fungsi konstan apabila untuk setiap $x$ elemen atau anggota bilangan Real($\Re$) fungsi tersebut akan memeberikan nilai yang tetap atau konstan.
Secara matematis fungsi konstan adalah suatu fungsi $f:A \to B$ dimana setiap anggota himpunan $A$ dipasangkan dengan satu anggota himpunan $B$ yang sama.
Akibatnya range dari fungsi tersebut hanyalah satu anggota.
Fungsi konstan diformulasikan dengan $f(x)=k, \ x \in \Re$ untuk sebuah $k$ merupakan konstanta atau tetapan.
Beberapa contoh yang merupakan sebuah fungsi konstan adalah :
- $f(x)=7$
- $f(x)=-5$
- $f(x)=3 \pi$
- dll.
2. Fungsi Identitas
Fungsi identitas adalah fungsi $f : A → A$ dengan $A$ sembarang himpunan tidak kosong.
Fungsi identitas diformulasikan dengan $f(x)=x$.
3. Fungsi Linier
Fungsi linier adalah sebuah fungsi berderajat satu dan lebih sering disebut juga dengan istilah fungsi garis.
Fungsi linier $f:\Re \to \Re$ diformulasikan $f(x)=ax+b$ untuk $a$, $b$ sebuah kontanta dan $a \neq 0$.
3. Fungsi Kuadrat
Ada fungsi berderajat satu tentu saja ada fungsi juga yang berderajat dua.
Yup, fungsi berderajat dua, fungsi kuadrat namanya.
Fungsi kuadrat $f:\Re \to \Re$ diformulasikan $f(x)=ax^{2}+bx+c$ dimana $a$, $b$ dan $c$ sebuah kontanta dan $a \neq 0$.
Beberapa contoh yang merupakan sebuah fungsi kuadrat adalah :
- $f(x)=x^{2}-4x+1$
- $f(x)=-5x^{2}+1+3x$
- $f(x)=3x^{2}-1$
- dll.
4. Fungsi Modulus
Fungsi modulus memang bakal terdengar asing ditelingamu.
Fungsi modulus memang lebih sering disebut dengan fungsi nilai mutlak.
Fungsi nilai mutlak adalah sebuah nama yang lebih membumi ditelinga kita.
Fungsi modulus $f:\Re \to \Re$ diformulasikan $f(x)=\big| x \big|$.
Beberapa contoh yang merupakan sebuah fungsi modulus adalah :
- $f(x)=\big| 4x-10 \big|$
- $f(x)=\big| 3x^{2}+2x-2 \big|$
- $f(x)=\big| x^{2}-1 \big|$
- dll.
5. Fungsi Ganjil dan Genap
Kamu ngga salah dengar kok...
Dalam matematika memang ada yang namanya fungsi ganjil dan genap.
Jadi yang bersifat ganjil dan genap tidak hanya bilangan atau angka saja.
Sebuah fungsi $f:\Re \to \Re$ disebut sebagai fungsi ganjil jika memenuhi $f(-x)=-f(x)$, dan fungsi genap jika memenuhi $f(-x)=f(x)$.
Beberapa contoh yang merupakan sebuah fungsi ganjil adalah :
- $f(x)=x^{3}$
- $f(x)=\sin x$
- $f(x)=\tan x$
- dll.
Beberapa contoh yang merupakan sebuah fungsi genap adalah :
- $f(x)=x^{2}$
- $f(x)=\cos x$
- $f(x)=\big| x \big|$
- dll.
5. Fungsi Injektif
Fungsi injektif atau yang lebih dikenal dengan istilah fungsi korespondensi satu - satu adalah sebuah fungsi dimana pada setiap anggota domain hanya boleh dipasangkan dengan satu anggota kodomain dan begitu pula sebaliknya.
Lebih jelas perhatikan diagram venn fungsi injektif berikut.
6. Fungsi Surjektif (Into)
Fungsi surjektif (into) dapat dikenali dengan mengamati daerah kodomain.
Seperti yang sudah dijelaskan diatas, bahwa range adalah himpunan bagian dari kodomain.
Jadi anggota kodomain belum tentu semuanya masuk anggota range.
Jika anggota kodomain tidak seluruhnya berpasangan dengan anggota domain, maka fungsi tersebut disebut dengan fungsi surjektif (into) atau fungsi ke dalam.
Perhatikan gambar diagram venn fungsi surjektif (into) di bawah ini.
6. Fungsi Surjektif (Onto)
Fungsi surjektif (onto) sering juga disebut dengan istilah fungsi kepada.
Fungsi surjektif (onto) adalah suatu fungsi dimana seluruh anggota kodomain memiliki pasangan.
Anggota kodomain boleh berpasangan lebih dari sekali.
Seluruh anggota kodomain merupakan range (daerah hasil).
Perhatikan gambar diagram venn fungsi surjektif (onto) di bawah ini.
7. Fungsi Bijektif
Fungsi bijektif berarti fungsi tersebut adalah merupakan fungsi injektif sekaligus fungsi surjektif.
Jadi fungsi bijektif adalah sebuah fungsi korespondensi satu - satu dimana daerah kodomain sekaligus merupakan range (daerah hasil) dari fungsi tersebut.
Perhatikan gambar diagram venn fungsi bijektif di bawah ini.
Kumpulan Soal dan Pembahasan Relasi dan Fungsi
Di bawah ini adalah kumpulan soal dan pembahasan materi relasi dan fungsi yang dirangkum dari berbagai sumber yang ada.Semua bakal jadi materi belajarmu agar kamu lebih memahami lagi konsep teori dari materi relasi dan fungsi.
Soal 1. Tugas Matematika
Domain dari fungsi $f(x)=\sqrt{3x+6}$ untuk setiap $x$ elemen himpunan bilangan Real adalah...
Syarat $f(x)$ terdefinisi pada setiap $x$ elemen himpunan bilangan Real adalah,
$ \begin{align} 3x+6 &\ge 0 \\ 3x &\ge -6 \\ x &\ge \dfrac{-6}{3} \\ x &\ge -2 \end{align} $
Jadi, domain dari fungsi $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \ge -2,x \in \Re \big \}$.
$ \begin{align} 3x+6 &\ge 0 \\ 3x &\ge -6 \\ x &\ge \dfrac{-6}{3} \\ x &\ge -2 \end{align} $
Jadi, domain dari fungsi $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \ge -2,x \in \Re \big \}$.
Soal 2. Ulangan Matematika
Domain dari fungsi $f(x)=\dfrac{x+1}{2x-8}$ untuk setiap $x$ elemen himpunan bilangan Real adalah...
Syarat $f(x)$ terdefinisi pada setiap $x$ elemen himpunan bilangan Real adalah,
$ \begin{align} 2x-8 &\ne 0 \\ 2x &\ne 8 \\ x &\ne \dfrac{8}{2} \\ x &\ne 4 \end{align} $
Jadi, domain dari fungsi $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \ne 4,x \in \Re \big \}$.
$ \begin{align} 2x-8 &\ne 0 \\ 2x &\ne 8 \\ x &\ne \dfrac{8}{2} \\ x &\ne 4 \end{align} $
Jadi, domain dari fungsi $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \ne 4,x \in \Re \big \}$.
Soal 3. Ulangan Matematika
Domain dari fungsi $f(x)=10-7x$ untuk setiap $x$ elemen himpunan bilangan Real adalah...
Karena $f(x)$ bakal terdefinisi untuk semua $x$ elemen himpunan bilangan Real maka domain dari $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \in \Re \big \}$.
$D_f=\big \{ x \ \big| \ x \in \Re \big \}$.
Soal 4. Tugas Matematika
Domain dari fungsi $f(x)=x^{2}-1$ untuk setiap $x$ elemen himpunan bilangan Real adalah...
Karena $f(x)$ bakal terdefinisi untuk semua $x$ elemen himpunan bilangan Real maka domain dari $f(x)$ adalah
$D_f=\big \{ x \ \big| \ x \in \Re \big \}$.
$D_f=\big \{ x \ \big| \ x \in \Re \big \}$.
Soal 5. Ulangan Matematika
Range dari fungsi $f(x)=2x^{2}-1$ untuk setiap $x$ elemen himpunan bilangan Real adalah...
Untuk mencari range dari sebuah fungsi kuadrat adalah kita cari dengan menghitung puncak maksimum atau minimumnya.
Fungsi $f(x)=2x^{2}-1$ adalah sebuah fungsi kuadrat yang mempunyai nilai minimum ($a \gt 0$).
Nilai $y_{min}$ dari fungsi kuadrat $f(x)=2x^{2}-1$ adalah,
$ \begin{align} y_{min} &= \dfrac{b^{2}-4ac}{-4a} \\ &= \dfrac{0^{2}-4(2)(-1)}{-4(2)} \\ &= \dfrac{8}{-8} \\ &= -1 \end{align} $
Jadi, range dari fungsi kuadrat $f(x)=2x^{2}-1$ adalah, $R_f=\big \{ y \ \big| y \ge -1,\ y \in \Re \big \}$.
Nilai $y_{min}$ dari fungsi kuadrat $f(x)=2x^{2}-1$ adalah,
$ \begin{align} y_{min} &= \dfrac{b^{2}-4ac}{-4a} \\ &= \dfrac{0^{2}-4(2)(-1)}{-4(2)} \\ &= \dfrac{8}{-8} \\ &= -1 \end{align} $
Jadi, range dari fungsi kuadrat $f(x)=2x^{2}-1$ adalah, $R_f=\big \{ y \ \big| y \ge -1,\ y \in \Re \big \}$.
Penutup
Nah sahabat kreatif, itulah rangkuman materi relasi dan fungsi kelas 10 SMA lengkap dengan soal dan pembahasannya.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !