30 Soal dan Pembahasan Pengetahuan Kuantitatif TPS SNBT
Ini adalah kumpulan soal dan pembahasan materi Pengetahuan Kuantitatif Tes Potensi Skolastik (TPS) pada SNBT.
Ngga terasa momen penentuan ujian masuk kampus atau yang sekarang kita kenal dengan SNBT (dulu UTBK) sudah semakin dekat.
Beberapa dari kalian pasti sudah berusaha sejak sekarang mempersiapkan belajar lebih bukan.
Salah satu kelompok uji dalam SNBT adalah tes kemampuan kuantitatif atau pengetahuan kuantitatif, dimana kelompok uji ini menuntut daya berhitung dari masing - masing peserta SNBT.
Pada dasarnya pengetahuan kuantitatif beberapa soal diantaranya ngga jauh beda sama soal matematika dasar jika pada penyelenggaraan tes masuk kampus yang dulu - dulu.
Nah beberapa materi di bawah ini bisa kalian asah jika kalian ingin mendapatkan hasil pengetahuan kuantitatif yang optimal.
Semoga dapat membantu meningkatkan belajar kalian dalam mempersiapkan diri menghadapi SNBT yang akan datang.
Ngga terasa momen penentuan ujian masuk kampus atau yang sekarang kita kenal dengan SNBT (dulu UTBK) sudah semakin dekat.
Beberapa dari kalian pasti sudah berusaha sejak sekarang mempersiapkan belajar lebih bukan.
Salah satu kelompok uji dalam SNBT adalah tes kemampuan kuantitatif atau pengetahuan kuantitatif, dimana kelompok uji ini menuntut daya berhitung dari masing - masing peserta SNBT.
Pada dasarnya pengetahuan kuantitatif beberapa soal diantaranya ngga jauh beda sama soal matematika dasar jika pada penyelenggaraan tes masuk kampus yang dulu - dulu.
Nah beberapa materi di bawah ini bisa kalian asah jika kalian ingin mendapatkan hasil pengetahuan kuantitatif yang optimal.
Materi sering muncul di Pengetahuan Kuantitatif, diantaranya :
- Operasi Bilangan.
- Himpunan.
- Perbandingan.
- Pola Bilangan.
- Geometri Sudut.
- Relasi dan Fungsi.
- Eksponen.
- Matriks.
- Statistika.
- Barisan dan Deret.
- Aritmatika sosial (laba, rugi, rabat, dll).
- Limit Fungsi.
- Pertidaksamaan. dll
Kumpulan Soal dan Pembahasan Pengetahuan Kuantitatif SNBT
Soal - soal di bawah ini dirangkum dari berbagai sumber termasuk di dalamnya soal - soal konstruksi kita sendiri semoga bermanfaat untuk melatih kemampuan kuantitaif kalian.
No.1 Simulasi Kuantiatif TPS SNBT
$a$#$b$@$c=a^2-b(a+c)$
Maka nilai dari $2$#$3$@$4$ adalah …
$ \begin{align} (A) \ -15 \\ (B) \ -14 \\ (C) \ -13 \\ (D) \ -12 \\ (E) \ -11 \\ \end{align} $
$a$#$b$@$c=a^2-b(a+c)$
Maka nilai dari $2$#$3$@$4$ adalah …
$ \begin{align} (A) \ -15 \\ (B) \ -14 \\ (C) \ -13 \\ (D) \ -12 \\ (E) \ -11 \\ \end{align} $
Dari bentuk $2$#$3$@$4$ kita dapatkan $a=2$, $b=3$ dan $c=4$.
Sehingga langkah berikutnya tinggal kita operasikan sesuai dengan operasi bilangan yang diketahui dalam soal.
$a$#$b$@$c=a^2-b(a+c)$
$2$#$3$@$4=2^2-3(2+4)=-14$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ -14$.
Sehingga langkah berikutnya tinggal kita operasikan sesuai dengan operasi bilangan yang diketahui dalam soal.
$a$#$b$@$c=a^2-b(a+c)$
$2$#$3$@$4=2^2-3(2+4)=-14$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ -14$.
No.2 Simulasi Kuantiatif TPS SNBT
Jika $a$∅$b=(b−a)2b−a$
Maka nilai dari $2$∅$1$ adalah …
$ \begin{align} &(A) \ 4 \\ &(B) \ 2 \\ &(C) \ 0 \\ &(D) \ -2 \\ &(E) \ -4 \\ \end{align} $
Jika $a$∅$b=(b−a)2b−a$
Maka nilai dari $2$∅$1$ adalah …
$ \begin{align} &(A) \ 4 \\ &(B) \ 2 \\ &(C) \ 0 \\ &(D) \ -2 \\ &(E) \ -4 \\ \end{align} $
Langsung operasikan sesuai dengan operasi bilangan yang diketahui.
$a$∅$b=(b−a)2b−a$
$2$∅$1=(1−2)2(1)−2=-4$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ -4$.
$a$∅$b=(b−a)2b−a$
$2$∅$1=(1−2)2(1)−2=-4$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ -4$.
No.3 Simulasi Kuantiatif TPS SNBT
$\dfrac{5^{4022}-5^{4018}}{5^{4020}-5^{4016}}=\cdots$
$ \begin{align} (A)\ & 1 \\ (B)\ & 3 \\ (C)\ & \dfrac{25}{4} \\ (D)\ & \dfrac{25}{2} \\ (E)\ & 25 \end{align} $
$\dfrac{5^{4022}-5^{4018}}{5^{4020}-5^{4016}}=\cdots$
$ \begin{align} (A)\ & 1 \\ (B)\ & 3 \\ (C)\ & \dfrac{25}{4} \\ (D)\ & \dfrac{25}{2} \\ (E)\ & 25 \end{align} $
$
\begin{align}
\dfrac{5^{4022}-5^{4018}}{5^{4020}-5^{4016}} &= \dfrac{5^{4018} \left( 5^{4} -1 \right)}{5^{4016} \left( 5^{4} -1 \right)} \\
&= \dfrac{5^{4018} }{5^{4016} } \\
&= 5^{4018-4016} \\
&= 5^{2}=25
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 25$.
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 25$.
No.4 Simulasi Kuantiatif TPS SNBT
Bila $x=36$ dan $y=125$ maka nilai $\dfrac{x^{-\frac{3}{2}}\ { \sqrt[3]{y^{2}}}}{y^{\frac{1}{3}} - x^{\frac{1}{2}}}$ adalah...
$\begin{align} (A)\ & -\dfrac{16}{216} \\ (B)\ & -\dfrac{25}{216} \\ (C)\ & -\dfrac{36}{216} \\ (D)\ & -\dfrac{49}{216} \\ (E)\ & -\dfrac{64}{216} \end{align}$
Bila $x=36$ dan $y=125$ maka nilai $\dfrac{x^{-\frac{3}{2}}\ { \sqrt[3]{y^{2}}}}{y^{\frac{1}{3}} - x^{\frac{1}{2}}}$ adalah...
$\begin{align} (A)\ & -\dfrac{16}{216} \\ (B)\ & -\dfrac{25}{216} \\ (C)\ & -\dfrac{36}{216} \\ (D)\ & -\dfrac{49}{216} \\ (E)\ & -\dfrac{64}{216} \end{align}$
Nilai $x$ dan $y$ bisa kita rubah menjadi $x=36=6^{2}$ dan $y=125=5^{3}$.
Sehingga,
$ \begin{align} & \dfrac{x^{-\frac{3}{2}}\ {\sqrt[3]{y^{2}}}}{y^{\frac{1}{3}} - x^{\frac{1}{2}}} \\ &= \dfrac{\left( 6^{2} \right)^{-\frac{3}{2}}\ \left( 5^{3} \right)^{ \frac{2}{3}}}{\left( 5^{3} \right)^{\frac{1}{3}} - \left( 6^{2} \right)^{\frac{1}{2}}} \\ &= \dfrac{\left( 6^{-3} \right)\ \left( 5^{2} \right)}{\left( 5^{1} \right) - \left( 6^{1} \right)} \\ &= \dfrac{ 25 }{6^{3} \left( -1 \right)} \\ &= -\dfrac{25}{216} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ -\dfrac{25}{216}$.
Sehingga,
$ \begin{align} & \dfrac{x^{-\frac{3}{2}}\ {\sqrt[3]{y^{2}}}}{y^{\frac{1}{3}} - x^{\frac{1}{2}}} \\ &= \dfrac{\left( 6^{2} \right)^{-\frac{3}{2}}\ \left( 5^{3} \right)^{ \frac{2}{3}}}{\left( 5^{3} \right)^{\frac{1}{3}} - \left( 6^{2} \right)^{\frac{1}{2}}} \\ &= \dfrac{\left( 6^{-3} \right)\ \left( 5^{2} \right)}{\left( 5^{1} \right) - \left( 6^{1} \right)} \\ &= \dfrac{ 25 }{6^{3} \left( -1 \right)} \\ &= -\dfrac{25}{216} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ -\dfrac{25}{216}$.
No.5 Simulasi Kuantiatif TPS SNBT
Jika $f(x+5)=x^2-5$ maka nilai dari $f^{-1}(11)$ adalah...
$\begin{align} &(A)\ 10 \\ &(B)\ 9 \\ &(C)\ 8 \\ &(D)\ 7 \\ &(E)\ 6 \end{align}$
Jika $f(x+5)=x^2-5$ maka nilai dari $f^{-1}(11)$ adalah...
$\begin{align} &(A)\ 10 \\ &(B)\ 9 \\ &(C)\ 8 \\ &(D)\ 7 \\ &(E)\ 6 \end{align}$
Dengan memakai kaidah definisi pada fungsi invers dimana,
$f(a)=b \iff f^{-1}(b)=a$.
Sehingga,
$f(x+5)=x^2-5$ akan memenuhi $f^{-1}(x^2-5)=x+5$.
Langkah berikutnya kita akan munculkan bentuk yang dicari yaitu $f^{-1}(11)$.
Caranya gimana???
Sederhana saja, kita bisa substitusi nilai $x=4$ kedalam persamaan $f^{-1}(x^2-5)=x+5$.
$x=4 \to f^{-1}(4^2-5)=4+5$.
Dengan demikian, $f^{-1}(11)=9$.
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 9$.
$f(a)=b \iff f^{-1}(b)=a$.
Sehingga,
$f(x+5)=x^2-5$ akan memenuhi $f^{-1}(x^2-5)=x+5$.
Langkah berikutnya kita akan munculkan bentuk yang dicari yaitu $f^{-1}(11)$.
Caranya gimana???
Sederhana saja, kita bisa substitusi nilai $x=4$ kedalam persamaan $f^{-1}(x^2-5)=x+5$.
$x=4 \to f^{-1}(4^2-5)=4+5$.
Dengan demikian, $f^{-1}(11)=9$.
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 9$.
No.6 Simulasi Kuantiatif TPS SNBT
Perhatikan gambar di bawah ini!
Besar penyiku sudut $AOC$ adalah...
$\begin{align} &(A)\ 50 \\ &(B)\ 40 \\ &(C)\ 20 \\ &(D)\ 15 \\ &(E)\ 10 \end{align}$
Perhatikan gambar di bawah ini!
Besar penyiku sudut $AOC$ adalah...
$\begin{align} &(A)\ 50 \\ &(B)\ 40 \\ &(C)\ 20 \\ &(D)\ 15 \\ &(E)\ 10 \end{align}$
$\begin{align}
\angle AOC + \angle BOC &= 180^{\circ} \\
2x+10 + 3x+20 &= 180^{\circ} \\
5x + 30 &= 180^{\circ} \\
5x &= 150^{\circ} \\
x &= 30^{\circ}
\end{align}$
Penyiku $\angle AOC$
$\begin{align} &= 90^{\circ}-\angle AOC \\ &= 90^{\circ}- \left( 2(30^{\circ})+10 \right) \\ &= 90^{\circ}-70^{\circ} \\ &= 20^{\circ} \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 20^{\circ}$.
Penyiku $\angle AOC$
$\begin{align} &= 90^{\circ}-\angle AOC \\ &= 90^{\circ}- \left( 2(30^{\circ})+10 \right) \\ &= 90^{\circ}-70^{\circ} \\ &= 20^{\circ} \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 20^{\circ}$.
No.7 Simulasi Kuantiatif TPS SNBT
Jika kuadrat jumlah dua bilangan $30$ sedangkan jumlah kuadrat kedua bilangan $20$ maka hasil kali keduanya adalah...
$\begin{align} &(A)\ 1 \\ &(B)\ 2 \\ &(C)\ 3 \\ &(D)\ 4 \\ &(E)\ 5 \end{align}$
Jika kuadrat jumlah dua bilangan $30$ sedangkan jumlah kuadrat kedua bilangan $20$ maka hasil kali keduanya adalah...
$\begin{align} &(A)\ 1 \\ &(B)\ 2 \\ &(C)\ 3 \\ &(D)\ 4 \\ &(E)\ 5 \end{align}$
Misal kedua bilangan yang dimaksud adalah $a$ dan $b$ maka diketahui pada soal,
$(a+b)^{2}=30$
$a^{2}+b^{2}=20$
Sehingga, $\begin{align} (a+b)^2 &= a^{2}+b^{2}+2ab \\ (a+b)^2 - \left( a^{2}+b^{2} \right) &= 2ab \\ 30-20 &= 2ab \\ 10 &= 2ab \\ ab &= 5 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5$.
$(a+b)^{2}=30$
$a^{2}+b^{2}=20$
Sehingga, $\begin{align} (a+b)^2 &= a^{2}+b^{2}+2ab \\ (a+b)^2 - \left( a^{2}+b^{2} \right) &= 2ab \\ 30-20 &= 2ab \\ 10 &= 2ab \\ ab &= 5 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5$.
No.8 Simulasi Kuantiatif TPS SNBT
$0 \lt x \lt 5$ dan $3 \lt y \lt 8$
Pernyataan berikut yang bernilai BENAR adalah...
$\begin{align} &(A)\ 5 \lt x+y \lt 8 \\ &(B)\ 3 \lt x+y \lt 5 \\ &(C)\ 5 \lt x+y \lt 11 \\ &(D)\ 3 \lt x+y \lt 13 \\ &(E)\ 5 \lt x+y \lt 13 \end{align}$
$0 \lt x \lt 5$ dan $3 \lt y \lt 8$
Pernyataan berikut yang bernilai BENAR adalah...
$\begin{align} &(A)\ 5 \lt x+y \lt 8 \\ &(B)\ 3 \lt x+y \lt 5 \\ &(C)\ 5 \lt x+y \lt 11 \\ &(D)\ 3 \lt x+y \lt 13 \\ &(E)\ 5 \lt x+y \lt 13 \end{align}$
Karena yang dicari adalah batas - batas interval dari $x+y$ maka cara mengerjakannya adalah jumlah saja batas - batas dari nilai $x$ dan $y$.
$0+3=3$
$0+8=8$
$5+3=8$
$5+8=13$.
Batas - batas interval dari $x+y$ tinggal kita ambil nilai minimum dan maksimum dari perhitungan di atas.
Nilai min $\to 3$
Nilai max $\to 13$.
Sehingga,
$3 \lt x+y \lt 13$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 3 \lt x+y \lt 13$.
$0+3=3$
$0+8=8$
$5+3=8$
$5+8=13$.
Batas - batas interval dari $x+y$ tinggal kita ambil nilai minimum dan maksimum dari perhitungan di atas.
Nilai min $\to 3$
Nilai max $\to 13$.
Sehingga,
$3 \lt x+y \lt 13$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 3 \lt x+y \lt 13$.
No.9 Simulasi Kuantiatif TPS SNBT
$1 \lt x \lt 4$ dan $-3 \lt y \lt 2$
Pernyataan berikut yang bernilai BENAR adalah...
$\begin{align} &(A)\ -12 \lt xy \lt 8 \\ &(B)\ -12 \lt xy \lt 2 \\ &(C)\ -3 \lt xy \lt 8 \\ &(D)\ -3 \lt xy \lt 2 \\ &(E)\ -2 \lt xy \lt 8 \end{align}$
$1 \lt x \lt 4$ dan $-3 \lt y \lt 2$
Pernyataan berikut yang bernilai BENAR adalah...
$\begin{align} &(A)\ -12 \lt xy \lt 8 \\ &(B)\ -12 \lt xy \lt 2 \\ &(C)\ -3 \lt xy \lt 8 \\ &(D)\ -3 \lt xy \lt 2 \\ &(E)\ -2 \lt xy \lt 8 \end{align}$
Karena yang dicari adalah batas - batas interval dari $xy$ maka cara mengerjakannya adalah kalikan saja batas - batas dari nilai $x$ dan $y$.
$1 \times (-3)=-3$
$1 \times 2=2$
$4 \times (-3)=-12$
$4 \times 2=8$.
Batas - batas interval dari $xy$ tinggal kita ambil nilai minimum dan maksimum dari perkalian di atas.
Nilai min $\to -12$
Nilai max $\to 8$.
Sehingga,
$-12 \lt xy \lt 8$.
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ -12 \lt xy \lt 8$.
$1 \times (-3)=-3$
$1 \times 2=2$
$4 \times (-3)=-12$
$4 \times 2=8$.
Batas - batas interval dari $xy$ tinggal kita ambil nilai minimum dan maksimum dari perkalian di atas.
Nilai min $\to -12$
Nilai max $\to 8$.
Sehingga,
$-12 \lt xy \lt 8$.
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ -12 \lt xy \lt 8$.
No.10 Simulasi Kuantiatif TPS SNBT
Selisih umur Paman dan Ayah saat ini adalah $15$ tahun. Jika perbandingan umur paman dan ayah sepuluh tahun yang lalu adalah $5 : 8$. Jumlah umur mereka dua puluh tahun mendatang adalah ...
$\begin{align} &(A)\ 125 \\ &(B)\ 120 \\ &(C)\ 115 \\ &(D)\ 110 \\ &(E)\ 105 \end{align}$
Selisih umur Paman dan Ayah saat ini adalah $15$ tahun. Jika perbandingan umur paman dan ayah sepuluh tahun yang lalu adalah $5 : 8$. Jumlah umur mereka dua puluh tahun mendatang adalah ...
$\begin{align} &(A)\ 125 \\ &(B)\ 120 \\ &(C)\ 115 \\ &(D)\ 110 \\ &(E)\ 105 \end{align}$
Misal Ayah ($A$) dan Paman ($P$) sehingga kita akan dapatkan persamaan :
$A-P=15$ .......... (i)
$\dfrac{P-10}{A-10}=\dfrac{5}{8}$
$8P-80=5A-50$
$5A-8P=-30$ .......... (ii)
Eliminasi (i) dan (ii),
$ \begin{array}{cc} A-P=15 & | \times 5 \\ 5A-8P=-30 & | \times 1 \\ \end{array} $
Kita peroleh,
$ \begin{array}{cc} 5A-5P=75 & \\ 5A-8P=-30 & (-) \\ \hline 3P=105 \\ P=35 \end{array} $
Substitusi ke (i),
$\begin{align} A-P&=15 \\ A-35&=15 \\ A&=50 \end{align}$
Dengan demikian jumlah umur ayah dan paman dua puluh tahun mendatang adalah :
$\begin{align} (A+20)+(P+20)&=(50+20)+(35+15) \\ &=70+50 \\ &= 120 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 120$.
$A-P=15$ .......... (i)
$\dfrac{P-10}{A-10}=\dfrac{5}{8}$
$8P-80=5A-50$
$5A-8P=-30$ .......... (ii)
Eliminasi (i) dan (ii),
$ \begin{array}{cc} A-P=15 & | \times 5 \\ 5A-8P=-30 & | \times 1 \\ \end{array} $
Kita peroleh,
$ \begin{array}{cc} 5A-5P=75 & \\ 5A-8P=-30 & (-) \\ \hline 3P=105 \\ P=35 \end{array} $
Substitusi ke (i),
$\begin{align} A-P&=15 \\ A-35&=15 \\ A&=50 \end{align}$
Dengan demikian jumlah umur ayah dan paman dua puluh tahun mendatang adalah :
$\begin{align} (A+20)+(P+20)&=(50+20)+(35+15) \\ &=70+50 \\ &= 120 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 120$.
No.11 Soal TPS UTBK 2019
Sepasang sepatu dibeli dengan harga $Rp. \ 200.000,00$. Diperlukan $Rp. \ 40.000,00$ untuk memperbaiki sol sepatu tersebut. Harga jual sepatu tersebut lebih tinggi daripada Rp300.000,00.Manakah hubungan yang benar antara kuantitas $P$ dan $Q$ berikut berdasarkan informasi yang diberikan?
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Sepasang sepatu dibeli dengan harga $Rp. \ 200.000,00$. Diperlukan $Rp. \ 40.000,00$ untuk memperbaiki sol sepatu tersebut. Harga jual sepatu tersebut lebih tinggi daripada Rp300.000,00.Manakah hubungan yang benar antara kuantitas $P$ dan $Q$ berikut berdasarkan informasi yang diberikan?
| $P$ | $Q$ |
|---|---|
| $20 \% $ | Persentase keuntungan penjualan sepatu tersebut. |
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Persentase keuntungan dari penjualan sepatu tersebut dapat kita peroleh dengan perhitungan melalui nilai harga jualnya.
Sayangnya di soal tidak diketahui dengan pasti berapa harga jual sepatunya, namun yang pasti bahwa nilai harga jual tersebut lebih tinggi dari $Rp. \ 300.000,00$.
Jika kita asumsikan bahwa harga jual sepatu tersebut $Rp. \ 300.000,00$, maka Q persentase keuntungan adalah :
$ \begin{align} Q &= \dfrac{60.000}{240.000} \times 100\% \\ & = \dfrac{1}{4} \times 100\% \\ & = 25\% \end{align} $
Karena dengan harga jual $Rp. \ 300.000,00$ nilai $P \lt Q$, untuk harga jual yang lebih dari $Rp. \ 300.000,00$ nilai $Q$ pasti akan bertambah besar dari nilai $P$.
Sehingga kesimpulan akhir yang bisa kita peroleh adalah $P \lt Q$.
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q$.
Sayangnya di soal tidak diketahui dengan pasti berapa harga jual sepatunya, namun yang pasti bahwa nilai harga jual tersebut lebih tinggi dari $Rp. \ 300.000,00$.
Jika kita asumsikan bahwa harga jual sepatu tersebut $Rp. \ 300.000,00$, maka Q persentase keuntungan adalah :
$ \begin{align} Q &= \dfrac{60.000}{240.000} \times 100\% \\ & = \dfrac{1}{4} \times 100\% \\ & = 25\% \end{align} $
Karena dengan harga jual $Rp. \ 300.000,00$ nilai $P \lt Q$, untuk harga jual yang lebih dari $Rp. \ 300.000,00$ nilai $Q$ pasti akan bertambah besar dari nilai $P$.
Sehingga kesimpulan akhir yang bisa kita peroleh adalah $P \lt Q$.
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q$.
No.12 Soal TPS UTBK 2019
Harga satu buku dan satu pensil $Rp. \ 55.000,00$. Selisih harga satu buku dan satu pensil adalah $Rp. \ 25.000,00$. Jika harga satu pensil adalah $a$. Manakah hubungan yang benar antara kuantitas $P$ dan $Q$ berikut berdasarkan informasi yang diberikan?
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Harga satu buku dan satu pensil $Rp. \ 55.000,00$. Selisih harga satu buku dan satu pensil adalah $Rp. \ 25.000,00$. Jika harga satu pensil adalah $a$. Manakah hubungan yang benar antara kuantitas $P$ dan $Q$ berikut berdasarkan informasi yang diberikan?
| $ \ \ P \ \ $ | $ \ \ Q \ \ $ |
|---|---|
| $ \ \ \ \ a \ \ \ \ $ | $20.000$ |
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Menyelesaikan soal di atas cukup mudah, kita bisa pakai eliminasi.
$ \begin{array}{c|c|cc} \text{Buku}+\text{Pensil}=Rp55.000,00 &\ \\ \text{Buku}-\text{Pensil}=Rp25.000,00 &\ (-) \\ \hline 2\text{Pensil}=Rp30.000,00 \\ \text{Pensil}=Rp15.000,00 = a \\ P=Rp15.000,00 \end{array} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q$.
$ \begin{array}{c|c|cc} \text{Buku}+\text{Pensil}=Rp55.000,00 &\ \\ \text{Buku}-\text{Pensil}=Rp25.000,00 &\ (-) \\ \hline 2\text{Pensil}=Rp30.000,00 \\ \text{Pensil}=Rp15.000,00 = a \\ P=Rp15.000,00 \end{array} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q$.
No.13 Soal TPS UTBK 2019
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan. Untuk membuat $300$ biskuit dengan ukuran dua kali biskuit kecil diperlukan adonan sebanyak ... kg
$ \begin{align} &(A)\ \dfrac{2}{5}x \\ &(B)\ \dfrac{5}{2}x \\ &(C)\ 2x \\ &(D)\ 5x \\ &(E)\ 10x \end{align} $
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan. Untuk membuat $300$ biskuit dengan ukuran dua kali biskuit kecil diperlukan adonan sebanyak ... kg
$ \begin{align} &(A)\ \dfrac{2}{5}x \\ &(B)\ \dfrac{5}{2}x \\ &(C)\ 2x \\ &(D)\ 5x \\ &(E)\ 10x \end{align} $
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan, artinya untuk membuat $1$ biskuit kecil dibutuhkan $\dfrac{x}{120}$ kg adonan.
Sehingga untuk membuat $300$ biskuit yang berukuran dua kali lebih besar,
$ \begin{align} &= 300 \times 2 \times \dfrac{x}{120} \\ &= \dfrac{600}{120}x \\ &= 5x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D)\ 5x $.
Sehingga untuk membuat $300$ biskuit yang berukuran dua kali lebih besar,
$ \begin{align} &= 300 \times 2 \times \dfrac{x}{120} \\ &= \dfrac{600}{120}x \\ &= 5x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D)\ 5x $.
No.14 Simulasi Kuantiatif TPS SNBT
Jika varian rasa baru tercipta dengan mencampurkan dua bahan rasa maka banyak varian rasa baru yang akan tercipta dari bahan - bahan Roy Chaniago adalah ... rasa.
$ \begin{align} & (A) \ 5 \\ & (B) \ 8 \\ & (C) \ 10 \\ & (D) \ 16 \\ & (E) \ 20 \end{align} $
Jika varian rasa baru tercipta dengan mencampurkan dua bahan rasa maka banyak varian rasa baru yang akan tercipta dari bahan - bahan Roy Chaniago adalah ... rasa.
$ \begin{align} & (A) \ 5 \\ & (B) \ 8 \\ & (C) \ 10 \\ & (D) \ 16 \\ & (E) \ 20 \end{align} $
Konsep yang digunakan untuk mengerjakan soal di atas adalah kombinasi.
Banyak semua bahan yang tersedia ada $5$ varian rasa, sedangkan varian rasa baru akan tercipta dengan mencampurkan $2$ varian rasa bahan yang ada.
Dengan demikian,
$ \begin{align} C_{2}^{5} &= \dfrac{5!}{(5-2)!2!} \\ &= \dfrac{3! \times 4 \times 5}{3!2!} \\ &= \dfrac{20}{2} \\ &= 10 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 10$ rasa baru.
Banyak semua bahan yang tersedia ada $5$ varian rasa, sedangkan varian rasa baru akan tercipta dengan mencampurkan $2$ varian rasa bahan yang ada.
Dengan demikian,
$ \begin{align} C_{2}^{5} &= \dfrac{5!}{(5-2)!2!} \\ &= \dfrac{3! \times 4 \times 5}{3!2!} \\ &= \dfrac{20}{2} \\ &= 10 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 10$ rasa baru.
No.15 Simulasi Kuantiatif TPS SNBT
Surya telah mengikuti $4$ tes Matematika dengan nilai berturut - turut $3$, $4$, $5$ dan $8$. Surya harus mengikuti $2$ kali tes lagi. Diketahui bahwa nilai setiap tes selalu berupa bilangan bulat dari $1$ sampai $10$. Jika salah satu dari dua nilai tes tersebut merupakan nilai sempurna sedangkan nilai satunya lagi paling rendah dan jangkauan dari keenam nilai tersebut sama dengan $\dfrac{2}{3}$ kali rata - ratanya maka pasangan nilai tes lainnya (nilai terendah) adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
Surya telah mengikuti $4$ tes Matematika dengan nilai berturut - turut $3$, $4$, $5$ dan $8$. Surya harus mengikuti $2$ kali tes lagi. Diketahui bahwa nilai setiap tes selalu berupa bilangan bulat dari $1$ sampai $10$. Jika salah satu dari dua nilai tes tersebut merupakan nilai sempurna sedangkan nilai satunya lagi paling rendah dan jangkauan dari keenam nilai tersebut sama dengan $\dfrac{2}{3}$ kali rata - ratanya maka pasangan nilai tes lainnya (nilai terendah) adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
Dua tes berikutnya dapat kita asumsikan $10$ (nilai sempurna) dan $x_{min}$ (nilai terendah) yang akan kita cari nilainya.
Sehingga jika keenam nilai tersebut kita urutkan kita akan dapatkan,
$x_{min}$, $3$, $4$, $5$, $8$, $10$.
Diketahui pula bahwa jangkauan nilai sama dengan $\dfrac{2}{3}$ kali rata - ratanya.
Dengan demikian,
$ \begin{align} J &= \dfrac{3}{2} \times \bar{x} \\ 10 - x_{min} &= \dfrac{3}{2} \left( \dfrac{x_{min}+3+4+5+8+10}{6} \right) \\ 10 - x_{min} &= \dfrac{3}{2} \left( \dfrac{x_{min}+30}{6} \right) \\ 10 - x_{min} &= \dfrac{x_{min}+30}{4} \\ 40-4x_{min} &= x_{min}+30 \\ 5x_{min} &= 10 \\ x_{min} &= 2 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 2$.
Sehingga jika keenam nilai tersebut kita urutkan kita akan dapatkan,
$x_{min}$, $3$, $4$, $5$, $8$, $10$.
Diketahui pula bahwa jangkauan nilai sama dengan $\dfrac{2}{3}$ kali rata - ratanya.
Dengan demikian,
$ \begin{align} J &= \dfrac{3}{2} \times \bar{x} \\ 10 - x_{min} &= \dfrac{3}{2} \left( \dfrac{x_{min}+3+4+5+8+10}{6} \right) \\ 10 - x_{min} &= \dfrac{3}{2} \left( \dfrac{x_{min}+30}{6} \right) \\ 10 - x_{min} &= \dfrac{x_{min}+30}{4} \\ 40-4x_{min} &= x_{min}+30 \\ 5x_{min} &= 10 \\ x_{min} &= 2 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 2$.
No.16 Simulasi Kuantiatif TPS SNBT
Sebuah kubus $ABCD.EFGH$ mempunyai rusuk 10 cm. Jika $K$ adalah titik perpotongan dua buah diagonal bidang $AH$ dan $DE$ maka jarak titik $B$ ke $K$ adalah ...
$ \begin{align} & (A) \ 5\sqrt{2} \\ & (B) \ 5\sqrt{3} \\ & (C) \ 10\sqrt{2} \\ & (D) \ 10\sqrt{3} \\ & (E) \ 5\sqrt{6} \end{align} $
Sebuah kubus $ABCD.EFGH$ mempunyai rusuk 10 cm. Jika $K$ adalah titik perpotongan dua buah diagonal bidang $AH$ dan $DE$ maka jarak titik $B$ ke $K$ adalah ...
$ \begin{align} & (A) \ 5\sqrt{2} \\ & (B) \ 5\sqrt{3} \\ & (C) \ 10\sqrt{2} \\ & (D) \ 10\sqrt{3} \\ & (E) \ 5\sqrt{6} \end{align} $
$K$ adalah titik tengah bidang samping kiri pada kubus $ABCD.EFGH$.
Dengan demikian,
$ \begin{align} &= \dfrac{1}{2} a \sqrt{6} \\ &= \dfrac{1}{2} 10 \sqrt{6} \\ &= 5\sqrt{6} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5\sqrt{6} $.
$TRIK \ SUPER \ KILAT \ !!!$
Jarak titik terhadap tengah - tengah bidang didepannya pada kubus $=\dfrac{1}{2} a \sqrt{6}$.
Jarak titik terhadap tengah - tengah bidang didepannya pada kubus $=\dfrac{1}{2} a \sqrt{6}$.
Dengan demikian,
$ \begin{align} &= \dfrac{1}{2} a \sqrt{6} \\ &= \dfrac{1}{2} 10 \sqrt{6} \\ &= 5\sqrt{6} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5\sqrt{6} $.
No.17 Simulasi Kuantiatif TPS SNBT
Nilai $m$ yang tepat untuk melengkapi pola di atas adalah ...
$ \begin{align} & (A) \ 1 \\ & (B) \ 2 \\ & (C) \ 3 \\ & (D) \ 4 \\ & (E) \ 5 \end{align} $
Nilai $m$ yang tepat untuk melengkapi pola di atas adalah ...
$ \begin{align} & (A) \ 1 \\ & (B) \ 2 \\ & (C) \ 3 \\ & (D) \ 4 \\ & (E) \ 5 \end{align} $
Pada pola segiempat gambar sebelah kiri mempunyai pola,
$13=(8 \times 2)-(5-2)$.
Sehingga pola segiempat yang sebelah kanan :
$17=(3 \times 7)-(8-m)$.
Dengan demikian nilai $m=4$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 4 $.
$13=(8 \times 2)-(5-2)$.
Sehingga pola segiempat yang sebelah kanan :
$17=(3 \times 7)-(8-m)$.
Dengan demikian nilai $m=4$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 4 $.
No.18 Simulasi Kuantiatif TPS SNBT
Nilai $Z$ yang tepat untuk melengkapi pola di bawah ini adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
Nilai $Z$ yang tepat untuk melengkapi pola di bawah ini adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
Jika kita perhatikan dengan seksama ternyata ada kesamaan operasi matematika pada kotak pertama dan kedua.
Dari kiri ke kanan, pola pada masing - masing kotak adalah :
Kotak I : $(5 \times 3)-(2 \times 6)=3$
Kotak II : $(6 \times 4)-(7 \times 3)=3$
Kotak III : $(4 \times Z)-(1 \times 5)=3$
Nilai $Z$ yang memenuhi adalah $Z=2$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 2 $.
Dari kiri ke kanan, pola pada masing - masing kotak adalah :
Kotak I : $(5 \times 3)-(2 \times 6)=3$
Kotak II : $(6 \times 4)-(7 \times 3)=3$
Kotak III : $(4 \times Z)-(1 \times 5)=3$
Nilai $Z$ yang memenuhi adalah $Z=2$.
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 2 $.
No.19 Simulasi Kuantiatif TPS SNBT
Nilai yang tepat untuk $x$ adalah ...
$ \begin{align} & (A) \ 10 \\ & (B) \ 9 \\ & (C) \ 8 \\ & (D) \ 7 \\ & (E) \ 6 \end{align} $
Nilai yang tepat untuk $x$ adalah ...
$ \begin{align} & (A) \ 10 \\ & (B) \ 9 \\ & (C) \ 8 \\ & (D) \ 7 \\ & (E) \ 6 \end{align} $
Hal pertama yang harus kita cermati adalah perbedaan jenis bangun datar pada pola di atas.
Sehingga untuk gambar pertama pola angka pada segi empat,
$ \begin{align} 9 &= \dfrac{2+10+8+16}{4} \end{align} $
Pola angka pada segitiga,
$ \begin{align} 8 &= \dfrac{12+5+7}{3} \end{align} $
Pola angka pada segi lima,
$ \begin{align} x &= \dfrac{1+20+6+10+3}{5} \\ &= \dfrac{40}{5} \\ &= 8 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 8 $.
Sehingga untuk gambar pertama pola angka pada segi empat,
$ \begin{align} 9 &= \dfrac{2+10+8+16}{4} \end{align} $
Pola angka pada segitiga,
$ \begin{align} 8 &= \dfrac{12+5+7}{3} \end{align} $
Pola angka pada segi lima,
$ \begin{align} x &= \dfrac{1+20+6+10+3}{5} \\ &= \dfrac{40}{5} \\ &= 8 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 8 $.
No.20 Simulasi Kuantiatif TPS SNBT
$A^{-1}=\begin{pmatrix} 2 & 5\\ 1 & 4 \end{pmatrix}$ memenuhi $\left( B^{-1} A \right)^{-1}=\begin{pmatrix} 3 & -6 \\ -1 & 6 \end{pmatrix}$ maka det($B$) adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
$A^{-1}=\begin{pmatrix} 2 & 5\\ 1 & 4 \end{pmatrix}$ memenuhi $\left( B^{-1} A \right)^{-1}=\begin{pmatrix} 3 & -6 \\ -1 & 6 \end{pmatrix}$ maka det($B$) adalah ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 4 \\ & (C) \ 3 \\ & (D) \ 2 \\ & (E) \ 1 \end{align} $
$
\begin{align}
\left( B^{-1} A \right)^{-1} &= \begin{pmatrix}
3 & -6 \\
-1 & 6
\end{pmatrix} \\
A^{-1} B &=\begin{pmatrix}
3 & -6 \\
-1 & 6
\end{pmatrix} \\
\begin{pmatrix}
2 & 5\\
1 & 4
\end{pmatrix} B &=\begin{pmatrix}
3 & -6 \\
-1 & 6
\end{pmatrix} \\
\begin{vmatrix}
2 & 5\\
1 & 4
\end{vmatrix} \times \text{det} \ (B) &= \begin{vmatrix}
3 & -6 \\
-1 & 6
\end{vmatrix} \\
3 \times \text{det} \ (B) &= 12 \\
\text{det} \ (B) &= 4
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 4 $.
$TRIK \ SUPER \ KILAT \ !!!$
$\text{det} \ (AB) = \text{det} \ (A) \times \text{det} \ (B)$
$\text{det} \ (AB) = \text{det} \ (A) \times \text{det} \ (B)$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 4 $.
No.21 Simulasi Kuantiatif TPS SNBT
Jika persamaan matriks $D^{-1}B^{-1}-D^{-1}C^{-1}=A$, $A \neq 0$.
Pernyataan yang setara dengan pernyataan di atas adalah ...
$ \begin{align} & (1) \ BD=CD \\ & (2) \ B=C \\ & (3) \ ABD=ACD \\ & (4) \ B^{-1}-C^{-1}=DA \end{align} $
Jika persamaan matriks $D^{-1}B^{-1}-D^{-1}C^{-1}=A$, $A \neq 0$.
Pernyataan yang setara dengan pernyataan di atas adalah ...
$ \begin{align} & (1) \ BD=CD \\ & (2) \ B=C \\ & (3) \ ABD=ACD \\ & (4) \ B^{-1}-C^{-1}=DA \end{align} $
Dengan menggunakan sifat dari identitas matriks, $A \cdot A^{-1} =I$ kita akan peroleh :
$ \begin{align} D^{-1}B^{-1}-D^{-1}C^{-1} &= A \\ D^{-1} \left( B^{-1}- C^{-1} \right) &= A \\ D \cdot D^{-1} \left( B^{-1}- C^{-1} \right) &= D \cdot A \\ I \cdot \left( B^{-1}- C^{-1} \right) &= D \cdot A \\ B^{-1}- C^{-1} &= D \cdot A \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) (4) \ B^{-1}-C^{-1}=DA $.
$ \begin{align} D^{-1}B^{-1}-D^{-1}C^{-1} &= A \\ D^{-1} \left( B^{-1}- C^{-1} \right) &= A \\ D \cdot D^{-1} \left( B^{-1}- C^{-1} \right) &= D \cdot A \\ I \cdot \left( B^{-1}- C^{-1} \right) &= D \cdot A \\ B^{-1}- C^{-1} &= D \cdot A \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) (4) \ B^{-1}-C^{-1}=DA $.
No.22 Simulasi Kuantiatif TPS SNBT
Jika $f(x)=3^{x-1}$ maka $f^{-1}(81)=\cdots$
$ \begin{align} & (A) \ 1 \\ & (B) \ 2 \\ & (C) \ 3 \\ & (D) \ 4 \\ & (E) \ 5 \end{align} $
Jika $f(x)=3^{x-1}$ maka $f^{-1}(81)=\cdots$
$ \begin{align} & (A) \ 1 \\ & (B) \ 2 \\ & (C) \ 3 \\ & (D) \ 4 \\ & (E) \ 5 \end{align} $
Dengan menggunakan konsep fungsi invers maka :
$ \begin{align} f(x)&= 3^{x-1} \\ \hline y &= 3^{x-1} \\ y &= 3^{x} \cdot 3^{-1} \\ 3y &= 3^{x} \\ x &= {}^3\!\log 3y \\ \hline f^{-1}(x) &= {}^3\!\log 3x \\ f^{-1}(81) &= {}^3\!\log 3(81) \\ &= {}^3\!\log 243 \\ &= {}^3\!\log 3^{5} \\ &= 5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5 $.
$ \begin{align} f(x)&= 3^{x-1} \\ \hline y &= 3^{x-1} \\ y &= 3^{x} \cdot 3^{-1} \\ 3y &= 3^{x} \\ x &= {}^3\!\log 3y \\ \hline f^{-1}(x) &= {}^3\!\log 3x \\ f^{-1}(81) &= {}^3\!\log 3(81) \\ &= {}^3\!\log 243 \\ &= {}^3\!\log 3^{5} \\ &= 5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 5 $.
No.23 Simulasi Kuantiatif TPS SNBT
$1,\ 3,\ 2,\ 6,\ 5,\ 15,\ 14,\ \cdots$
Nilai yang TEPAT untuk melengkapi pola bilangan di atas adalah ...
$ \begin{align} & (A) \ 24 \\ & (B) \ 28 \\ & (C) \ 32 \\ & (D) \ 42 \\ & (E) \ 52 \end{align} $
$1,\ 3,\ 2,\ 6,\ 5,\ 15,\ 14,\ \cdots$
Nilai yang TEPAT untuk melengkapi pola bilangan di atas adalah ...
$ \begin{align} & (A) \ 24 \\ & (B) \ 28 \\ & (C) \ 32 \\ & (D) \ 42 \\ & (E) \ 52 \end{align} $
No.24 Simulasi Kuantiatif TPS SNBT
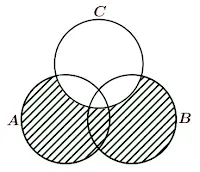
Daerah yang di arsir pada diagram venn di atas menyatakan himpunan dari ...
$ \begin{align} & (A) \ (A \cup B) \cap C \\ & (B) \ (A \cup B) - C \\ & (C) \ (A \cap B) \cup C \\ & (D) \ C - (A \cup B) \\ & (E) \ A - (B \cap C) \end{align} $
Daerah yang di arsir pada diagram venn di atas menyatakan himpunan dari ...
$ \begin{align} & (A) \ (A \cup B) \cap C \\ & (B) \ (A \cup B) - C \\ & (C) \ (A \cap B) \cup C \\ & (D) \ C - (A \cup B) \\ & (E) \ A - (B \cap C) \end{align} $
Daerah yang di arsir sebenarnya merupakan daerah gabungan antara himpunan $A$ dan $B$ yang sebagian hilang (dikurangi) pada bagian himpunan $C$.
Sehingga,
$(A \cup B) - C$
Untuk lebih jelasnya silahkan pahami dua operasi himpunan berikut gambar diagramnya di bawah ini.
(1) Gabungan Himpunan
Merupakan gabungan dari dua buah himpunan baik sebagian atau seluruhnya.
Disimbolkan dengan simbol " $\cup$ ".
(1) Pengurangan Himpunan
Merupakan daerah hasil pengurangan dari dua buah himpunan baik sebagian atau seluruhnya.
Disimbolkan dengan simbol " $-$ ".
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ (A \cup B) - C $.
Sehingga,
$(A \cup B) - C$
Untuk lebih jelasnya silahkan pahami dua operasi himpunan berikut gambar diagramnya di bawah ini.
(1) Gabungan Himpunan
Merupakan gabungan dari dua buah himpunan baik sebagian atau seluruhnya.
Disimbolkan dengan simbol " $\cup$ ".
(1) Pengurangan Himpunan
Merupakan daerah hasil pengurangan dari dua buah himpunan baik sebagian atau seluruhnya.
Disimbolkan dengan simbol " $-$ ".
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ (A \cup B) - C $.
No.25 Simulasi Kuantiatif TPS SNBT
Dalam suatu penelitian pemakaian $45$ ibu-ibu terhadap dua jenis produk sabun, yaitu sabun $A$ dan sabun $B$. Sebanyak $30$ orang menggunakan produk jenis sabun $A$, $25$ orang menggunakan jenis sabun $B$, dan $2$ orang tidak menggunakan kedua jenis sabun tersebut. Banyak ibu - ibu yang hanya menggunakan sabun $A$ saja adalah....
$ \begin{align} & (A) \ 20 \\ & (B) \ 18 \\ & (C) \ 12 \\ & (D) \ 8 \\ & (E) \ 2 \end{align} $
Dalam suatu penelitian pemakaian $45$ ibu-ibu terhadap dua jenis produk sabun, yaitu sabun $A$ dan sabun $B$. Sebanyak $30$ orang menggunakan produk jenis sabun $A$, $25$ orang menggunakan jenis sabun $B$, dan $2$ orang tidak menggunakan kedua jenis sabun tersebut. Banyak ibu - ibu yang hanya menggunakan sabun $A$ saja adalah....
$ \begin{align} & (A) \ 20 \\ & (B) \ 18 \\ & (C) \ 12 \\ & (D) \ 8 \\ & (E) \ 2 \end{align} $
Kita gunakan rumus kardinalitas himpunan untuk mengerjakan soal di atas.
Kardinalitas himpunan adalah bilangan yang menyatakan banyaknya anggota dari suatu himpunan yang disnotasikan dengan $n(A)$.
Misal :
$A \to$ himpunan ibu - ibu memakai sabun $A$.
$B \to$ himpunan ibu - ibu memakai sabun $B$.
Sehingga,
$ \begin{align} n(A \cup B) &= n(A)+n(B)-n(A \cap B) + n(A \cup B)^{c} \\ 45 &= 30+25-x+2 \\ 45 &= 57 - x \\ x &= 12 \end{align} $
Banyak ibu - ibu yang memakai sabun $A$ dan $B$ bersamaan ada sebanyak $12$ orang.
Dengan demikian banyak ibu - ibu yang hanya memakai sabun $A$ saja,
$ \begin{align} &= 30-12 \\ &= 18 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 18$.
Kardinalitas himpunan adalah bilangan yang menyatakan banyaknya anggota dari suatu himpunan yang disnotasikan dengan $n(A)$.
Misal :
$A \to$ himpunan ibu - ibu memakai sabun $A$.
$B \to$ himpunan ibu - ibu memakai sabun $B$.
Sehingga,
$ \begin{align} n(A \cup B) &= n(A)+n(B)-n(A \cap B) + n(A \cup B)^{c} \\ 45 &= 30+25-x+2 \\ 45 &= 57 - x \\ x &= 12 \end{align} $
Banyak ibu - ibu yang memakai sabun $A$ dan $B$ bersamaan ada sebanyak $12$ orang.
Dengan demikian banyak ibu - ibu yang hanya memakai sabun $A$ saja,
$ \begin{align} &= 30-12 \\ &= 18 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ 18$.
No.26 Simulasi Kuantiatif TPS SNBT
Anton memiliki password yang terdiri dari satu huruf diantara huruf - huruf konsonan $k$, $m$, $p$, $s$, $t$ dan $v$. Peluang Anton salah dalam mengetikkan password nya adalah....
$ \begin{align} & (A) \ \dfrac{5}{6} \\ & (B) \ \dfrac{1}{6} \\ & (C) \ \dfrac{1}{2} \\ & (D) \ \dfrac{3}{4} \\ & (E) \ \dfrac{1}{4} \end{align} $
Anton memiliki password yang terdiri dari satu huruf diantara huruf - huruf konsonan $k$, $m$, $p$, $s$, $t$ dan $v$. Peluang Anton salah dalam mengetikkan password nya adalah....
$ \begin{align} & (A) \ \dfrac{5}{6} \\ & (B) \ \dfrac{1}{6} \\ & (C) \ \dfrac{1}{2} \\ & (D) \ \dfrac{3}{4} \\ & (E) \ \dfrac{1}{4} \end{align} $
Peluang Anton benar dalam mengetikkan password nya adalah $\dfrac{1}{6}$.
Sehingga besar peluang Anton salah dalam mengetikkan passwordnya,
$ \begin{align} &= 1-\dfrac{1}{6} \\ &= \dfrac{5}{6} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ \dfrac{5}{6}$.
Sehingga besar peluang Anton salah dalam mengetikkan passwordnya,
$ \begin{align} &= 1-\dfrac{1}{6} \\ &= \dfrac{5}{6} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ \dfrac{5}{6}$.
No.27 Simulasi Kuantiatif TPS SNBT
Peluang Ali sukses menahan bola masuk ke gawang pada sebuah tendangan pinalti adalah $\dfrac{2}{3}$. Jika pertandingan tersebut membutuhkan $4$ kali tendangan pinalti untuk menentukan tim mana yang akan memenangkan pertandingan maka peluang Ali gagal menahan bola tepat $1$ kali dalam adu pinalti tersebut adalah...
$ \begin{align} & (A) \ \dfrac{16}{81} \\ & (B) \ \dfrac{20}{81} \\ & (C) \ \dfrac{29}{81} \\ & (D) \ \dfrac{32}{81} \\ & (E) \ \dfrac{64}{81} \end{align} $
Peluang Ali sukses menahan bola masuk ke gawang pada sebuah tendangan pinalti adalah $\dfrac{2}{3}$. Jika pertandingan tersebut membutuhkan $4$ kali tendangan pinalti untuk menentukan tim mana yang akan memenangkan pertandingan maka peluang Ali gagal menahan bola tepat $1$ kali dalam adu pinalti tersebut adalah...
$ \begin{align} & (A) \ \dfrac{16}{81} \\ & (B) \ \dfrac{20}{81} \\ & (C) \ \dfrac{29}{81} \\ & (D) \ \dfrac{32}{81} \\ & (E) \ \dfrac{64}{81} \end{align} $
Gunakan konsep dari Peluang Distribusi Binomial untuk mengerjakannya.
Peluang sukses ($p$) $=\dfrac{2}{3}$.
Peluang gagal ($q$) $=1-\dfrac{2}{3}=\dfrac{1}{3}$.
Peluang $3$ kali sukses dan $1$ gagal menahan bola ke gawang,
$ \begin{align} P(X=x) &= \binom{n}{x} \ p^{x} \ q^{n-x} \\ P(X=3) &= \binom{4}{3} \ \left( \dfrac{2}{3} \right)^{3} \ \left( \dfrac{1}{3} \right)^{4-3} \\ &= \binom{4}{3} \ \left( \dfrac{2}{3} \right)^{3} \ \left( \dfrac{1}{3} \right)^{1} \\ &= \dfrac{4!}{1!3!} \ \left( \dfrac{8}{27} \right) \ \left( \dfrac{1}{3} \right) \\ &= 4 \ \ \left( \dfrac{8}{81} \right) \\ &= \dfrac{32}{81} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ \dfrac{32}{81}$.
Peluang sukses ($p$) $=\dfrac{2}{3}$.
Peluang gagal ($q$) $=1-\dfrac{2}{3}=\dfrac{1}{3}$.
Peluang $3$ kali sukses dan $1$ gagal menahan bola ke gawang,
$ \begin{align} P(X=x) &= \binom{n}{x} \ p^{x} \ q^{n-x} \\ P(X=3) &= \binom{4}{3} \ \left( \dfrac{2}{3} \right)^{3} \ \left( \dfrac{1}{3} \right)^{4-3} \\ &= \binom{4}{3} \ \left( \dfrac{2}{3} \right)^{3} \ \left( \dfrac{1}{3} \right)^{1} \\ &= \dfrac{4!}{1!3!} \ \left( \dfrac{8}{27} \right) \ \left( \dfrac{1}{3} \right) \\ &= 4 \ \ \left( \dfrac{8}{81} \right) \\ &= \dfrac{32}{81} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ \dfrac{32}{81}$.
No.28 Simulasi Kuantiatif TPS SNBT
Jika rata - rata $7$ bilangan adalah $8$ dan rata - rata $4$ bilangan adalah $9$.
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ P+Q=75.000 \\ &(E)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Jika rata - rata $7$ bilangan adalah $8$ dan rata - rata $4$ bilangan adalah $9$.
| $P$ | $Q$ |
|---|---|
| rata - rata gabungan kedua kelompok bilangan | $8,5$ |
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ P+Q=75.000 \\ &(E)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Rata - rata gabungan kedua kelompok bilangan,
$\begin{align} \bar{x}_{gabungan} &= \dfrac{(7 \times 8) + (4 \times 9)}{7+4} \\ &= \dfrac{56+36}{11} \\ &= \dfrac{92}{11} \\ &= 8,36 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q $.
$\begin{align} \bar{x}_{gabungan} &= \dfrac{(7 \times 8) + (4 \times 9)}{7+4} \\ &= \dfrac{56+36}{11} \\ &= \dfrac{92}{11} \\ &= 8,36 \end{align}$
Jadi, pilihan jawaban yang TEPAT adalah $(B) \ P \lt Q $.
No.29 Simulasi Kuantiatif TPS SNBT
$3$ ekor sapi dapat menghabiskan rumput pada sebidang lahan dalam $20$ hari, sedangkan $5$ ekor kambing membutuhkan waktu $40$ hari. Berapa hari rumput tersebut akan habis jika dimakan oleh 2 ekor sapi dan 2 ekor kambing?
$ \begin{align} & (A) \ 10 \ \text{hari} \\ & (B) \ 17 \ \text{hari} \\ & (C) \ 23 \ \text{hari} \\ & (D) \ 25 \ \text{hari} \\ & (E) \ 30 \ \text{hari} \end{align} $
$3$ ekor sapi dapat menghabiskan rumput pada sebidang lahan dalam $20$ hari, sedangkan $5$ ekor kambing membutuhkan waktu $40$ hari. Berapa hari rumput tersebut akan habis jika dimakan oleh 2 ekor sapi dan 2 ekor kambing?
$ \begin{align} & (A) \ 10 \ \text{hari} \\ & (B) \ 17 \ \text{hari} \\ & (C) \ 23 \ \text{hari} \\ & (D) \ 25 \ \text{hari} \\ & (E) \ 30 \ \text{hari} \end{align} $
Misalkan Sapi = $A$ dan Kambing = $B$ maka,
$\clubsuit$
$\dfrac{3}{A} = \dfrac{1}{20} \to A = 60$
$\clubsuit$$\clubsuit$
$\dfrac{5}{B} = \dfrac{1}{40} \to B = 200$
Sehingga jika sapi dan kambing bekerja sama maka,
$ \begin{align} 2A+2B &= \dfrac{1}{\frac{2}{60}+\frac{2}{200}} \\ &= \dfrac{1}{\frac{20}{600}+\frac{6}{600}} \\ &= \dfrac{600}{26} \\ &= 23 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 23 $ hari.
$\clubsuit$
$\dfrac{3}{A} = \dfrac{1}{20} \to A = 60$
$\clubsuit$$\clubsuit$
$\dfrac{5}{B} = \dfrac{1}{40} \to B = 200$
Sehingga jika sapi dan kambing bekerja sama maka,
$ \begin{align} 2A+2B &= \dfrac{1}{\frac{2}{60}+\frac{2}{200}} \\ &= \dfrac{1}{\frac{20}{600}+\frac{6}{600}} \\ &= \dfrac{600}{26} \\ &= 23 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 23 $ hari.
No.30 Simulasi Kuantiatif TPS SNBT
Jika $A= \{x|-2 \gt x \gt 2, x \in \Re \}$ dan $B= \{x|x \ \text{bilangan prima} \ \lt 8 \}$.
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ P+Q=5 \\ &(E)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
Jika $A= \{x|-2 \gt x \gt 2, x \in \Re \}$ dan $B= \{x|x \ \text{bilangan prima} \ \lt 8 \}$.
| $P$ | $Q$ |
|---|---|
| Banyak pemetaan dari $A$ ke $B$ | Banyak pemetaan dari $B$ ke $A$ |
$\begin{align} &(A)\ P \gt Q \\ &(B)\ P \lt Q \\ &(C)\ P=Q \\ &(D)\ P+Q=5 \\ &(E)\ \text{Informasi yang diberikan tidak cukup} \\ & \text{untuk memutuskan jawaban soal di atas.} \\ \end{align}$
$A= \{x|-2 \gt x \gt 2, x \in Z \}$
$A= \{x|-1 ,0, 1, x \in Z \} \to n(A)=3$
$B= \{x|x \ \text{bilangan prima} \ \lt 8 \}$
$B= \{x|2 ,3, 5, 7 \} \to n(B)=4$
$P \to$ Banyak pemetaan dari $A$ ke $B$,
$ \begin{align} n(B)^{n(A)} &= 4^{3} \\ &= 64 \end{align} $
$Q \to$ Banyak pemetaan dari $B$ ke $A$,
$ \begin{align} n(A)^{n(B)} &= 3^{4} \\ &= 81 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B)\ P \lt Q$.
$A= \{x|-1 ,0, 1, x \in Z \} \to n(A)=3$
$B= \{x|x \ \text{bilangan prima} \ \lt 8 \}$
$B= \{x|2 ,3, 5, 7 \} \to n(B)=4$
$P \to$ Banyak pemetaan dari $A$ ke $B$,
$ \begin{align} n(B)^{n(A)} &= 4^{3} \\ &= 64 \end{align} $
$Q \to$ Banyak pemetaan dari $B$ ke $A$,
$ \begin{align} n(A)^{n(B)} &= 3^{4} \\ &= 81 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B)\ P \lt Q$.
Penutup
Nah sahabat kreatif, itulah 30 kumpulan soal dan pembahasan materi pengetahuan kuantitatif TPS SNBT.Semoga dapat membantu meningkatkan belajar kalian dalam mempersiapkan diri menghadapi SNBT yang akan datang.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !
“Orang bijak belajar ketika mereka bisa. Orang bodoh baru belajar ketika terpaksa.” – Arthur Wellesey