40 Kumpulan Soal Matematika Wajib PSAJ Kelas 12 SMA Tahun 2024
Ini adalah kumpulan soal Penilaian Sumatif Akhir Jenjang (PSAJ) mata pelajaran matematika wajib lengkap dengan pembahasan perbutir soal.
Penilaian Sumatif Akhir Jenjang (PSAJ) merupakan kegiatan penting yang dilakukan oleh sekolah untuk menilai pencapaian standar kompetensi lulusan di semua mata pelajaran yang dijalankan sesuai dengan kurikulum yang berlaku.
Tujuannya adalah untuk mengukur sejauh mana siswa telah mencapai kompetensi yang ditetapkan dalam setiap mata pelajaran.
Dalam pelajaran matematika wajib materi - materi yang diujikan meliputi gabungan dari materi yang telah diberikan saat kelas 10, 11 dan kelas 12 SMA.
Terkait proporsinya tentu saja materi yang diberikan saat kelas 12 akan lebih banyak dibanding dengan materi matematika wajib kelas 10 dan kelas 11 SMA.
Di bawah ini kita akan bahas kumpulan soal yang merupakan kisi - kisi dari Penilaian Sumatif Akhir Jenjang (PSAJ) mata pelajaran matematika wajib yang berhasil dihimpun dari berbagai sumber yang bisa membantu kalian dalam mempersiapkan diri untuk menghadapinya.
Simak hingga akhir ya.
Semoga bisa menjadi bahan belajar, bahan latihan yang baik buat kalian yang sedang mempersiapkan diri mengikuti Penilaian Sumatif Akhir Jenjang (PSAJ).
Penilaian Sumatif Akhir Jenjang (PSAJ) merupakan kegiatan penting yang dilakukan oleh sekolah untuk menilai pencapaian standar kompetensi lulusan di semua mata pelajaran yang dijalankan sesuai dengan kurikulum yang berlaku.
Tujuannya adalah untuk mengukur sejauh mana siswa telah mencapai kompetensi yang ditetapkan dalam setiap mata pelajaran.
Dalam pelajaran matematika wajib materi - materi yang diujikan meliputi gabungan dari materi yang telah diberikan saat kelas 10, 11 dan kelas 12 SMA.
Terkait proporsinya tentu saja materi yang diberikan saat kelas 12 akan lebih banyak dibanding dengan materi matematika wajib kelas 10 dan kelas 11 SMA.
Di bawah ini kita akan bahas kumpulan soal yang merupakan kisi - kisi dari Penilaian Sumatif Akhir Jenjang (PSAJ) mata pelajaran matematika wajib yang berhasil dihimpun dari berbagai sumber yang bisa membantu kalian dalam mempersiapkan diri untuk menghadapinya.
Simak hingga akhir ya.
Soal Matematika Wajib PSAJ Kelas 12 SMA
No. 1 Sistem Persamaan Linear Dua Variabel (SPLDV)
Harga $4$ kemeja dan $3$ kaos adalah $Rp. \ 250.000,00$. Sedangkan harga $2$ kemeja dan $7$ kaos adalah $Rp.\ 290.000,00$. Harga $2$ kemeja adalah...
$ \begin{align} & (A) \ Rp. \ 58.000,00 \\ & (B) \ Rp. \ 65.000,00 \\ & (C) \ Rp. \ 70.000,00 \\ & (D) \ Rp. \ 80.000,00 \\ & (E) \ Rp. \ 85.000,00 \end{align} $
Harga $4$ kemeja dan $3$ kaos adalah $Rp. \ 250.000,00$. Sedangkan harga $2$ kemeja dan $7$ kaos adalah $Rp.\ 290.000,00$. Harga $2$ kemeja adalah...
$ \begin{align} & (A) \ Rp. \ 58.000,00 \\ & (B) \ Rp. \ 65.000,00 \\ & (C) \ Rp. \ 70.000,00 \\ & (D) \ Rp. \ 80.000,00 \\ & (E) \ Rp. \ 85.000,00 \end{align} $
Misalkan saja $x \to$ menyatakan banyak kemeja dan $y \to$ banyak kaos, maka kita akan dapatkan dua persamaan yang diketahui di soal yaitu :
$4x+3y=250.000$
$2x+7y=290.000$
Untuk menyelesaikannya kita bisa langsung eliminasi kedua persamaan di atas, kita peroleh :
$ \begin{array}{cc} 4x+3y=250.000 & | \times 7 \\ 2x+7y=290.000 & | \times 3 \\ \end{array} $
Sehingga,
$ \begin{array}{cc} 28x+21y=1.750.000 & \\ 6x+21y=870.000 & (-) \\ \hline 22x=880.000 \\ 2x=80.000 \end{array} $
Jadi, harga $2$ kemeja ($2x$) adalah $Rp. \ 80.000,00$ sesuai pilihan jawaban $(D.)$.
$4x+3y=250.000$
$2x+7y=290.000$
Untuk menyelesaikannya kita bisa langsung eliminasi kedua persamaan di atas, kita peroleh :
$ \begin{array}{cc} 4x+3y=250.000 & | \times 7 \\ 2x+7y=290.000 & | \times 3 \\ \end{array} $
Sehingga,
$ \begin{array}{cc} 28x+21y=1.750.000 & \\ 6x+21y=870.000 & (-) \\ \hline 22x=880.000 \\ 2x=80.000 \end{array} $
Jadi, harga $2$ kemeja ($2x$) adalah $Rp. \ 80.000,00$ sesuai pilihan jawaban $(D.)$.
No. 2 Sistem Persamaan Linear Dua Variabel (SPLDV)
Harga delapan buah mangga dan dua buah jeruk adalah $Rp.\ 17.000,00$, sedangkan harga enam buah mangga dan empat buah jeruk adalah $Rp.\ 19.000,00$. Harga sebuah mangga adalah...
$ \begin{align} & (A) \ Rp. \ 1.500,00 \\ & (B) \ Rp. \ 2.500,00 \\ & (C) \ Rp. \ 3.000,00 \\ & (D) \ Rp. \ 3.200,00 \\ & (E) \ Rp. \ 3.500,00 \end{align} $
Harga delapan buah mangga dan dua buah jeruk adalah $Rp.\ 17.000,00$, sedangkan harga enam buah mangga dan empat buah jeruk adalah $Rp.\ 19.000,00$. Harga sebuah mangga adalah...
$ \begin{align} & (A) \ Rp. \ 1.500,00 \\ & (B) \ Rp. \ 2.500,00 \\ & (C) \ Rp. \ 3.000,00 \\ & (D) \ Rp. \ 3.200,00 \\ & (E) \ Rp. \ 3.500,00 \end{align} $
Misalkan saja $m \to$ menyatakan banyak buah mangga dan $j \to$ banyak buah jeruk, maka kita akan dapatkan dua persamaan yang diketahui di soal yaitu :
$8m+2j=17.000$
$6m+4j=19.000$
Untuk menyelesaikannya kita bisa langsung eliminasi kedua persamaan di atas, kita peroleh :
$ \begin{array}{cc} 8m+2j=17.000 & | \times 2 \\ 6m+4j=19.000 & | \times 1 \\ \end{array} $
Sehingga,
$ \begin{array}{cc} 16m+4j=34.000 & \\ 6m+4j=19.000 & (-) \\ \hline 10m=15.000 \\ m=1.500 \end{array} $
Jadi, harga sebuah mangga ($m$) adalah $Rp. \ 1.500,00$ sesuai pilihan jawaban $(A.)$.
$8m+2j=17.000$
$6m+4j=19.000$
Untuk menyelesaikannya kita bisa langsung eliminasi kedua persamaan di atas, kita peroleh :
$ \begin{array}{cc} 8m+2j=17.000 & | \times 2 \\ 6m+4j=19.000 & | \times 1 \\ \end{array} $
Sehingga,
$ \begin{array}{cc} 16m+4j=34.000 & \\ 6m+4j=19.000 & (-) \\ \hline 10m=15.000 \\ m=1.500 \end{array} $
Jadi, harga sebuah mangga ($m$) adalah $Rp. \ 1.500,00$ sesuai pilihan jawaban $(A.)$.
No. 3 Pertidaksamaan Kuadrat
Himpunan penyelesaian dari pertidaksamaan $x^{2}-4x-5 \le 0$ adalah...
$ \begin{align} & (A) \ -1 \le x \le 5 \\ & (B) \ 0 \le x \le 5 \\ & (C) \ x \le 1 \ \text{atau} \ x \ge 4 \\ & (D) \ x \le -1 \ \text{atau} \ x \ge 5 \\ & (E) \ x \le 0 \ \text{atau} \ x \ge 5 \end{align} $
Himpunan penyelesaian dari pertidaksamaan $x^{2}-4x-5 \le 0$ adalah...
$ \begin{align} & (A) \ -1 \le x \le 5 \\ & (B) \ 0 \le x \le 5 \\ & (C) \ x \le 1 \ \text{atau} \ x \ge 4 \\ & (D) \ x \le -1 \ \text{atau} \ x \ge 5 \\ & (E) \ x \le 0 \ \text{atau} \ x \ge 5 \end{align} $
$
\begin{align}
x^{2}-4x-5 & \le 0 \\
(x-5)(x+1) & \le 0 \\
-1 \le x & \le 5
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ -1 \le x \le 5$.
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ -1 \le x \le 5$.
No. 4 Program Linear
Luas daerah parkir $1.760$ $m^{2}$ luas rata-rata untuk mobil kecil $4$ $m^{2}$ dan mobil besar $20$ $m^{2}$. Daya tampung maksimum hanya $200$ kendaraan, biaya parkir mobil kecil $Rp. \ 1.000,00$/jam dan mobil besar $Rp.\ 2.000,00$/jam. Diketahui $x$ menyatakan banyak mobil kecil dan $y$ menyatakan banyak mobil besar yang parkir. Jika dalam satu jam terisi penuh dan tidak ada kendaran yang pergi dan datang, model matematika dari masalah diatas adalah...
$ \begin{align} & (A) \ 4x+20y \le 1.750; \ x+y \ge 200; \ x \le 0; \ y \ge 0 \\ & (B) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \ge 0; \ y \ge 0 \\ & (C) \ 4x+20y \ge 1.750; \ x+y \le 200; \ x \le 0; \ y \ge 0 \\ & (D) \ 4x+20y \ge 1.750; \ x+y \le 200; \ x \ge 0; \ y \le 0 \\ & (E) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \le 0; \ y \le 0 \end{align} $
Luas daerah parkir $1.760$ $m^{2}$ luas rata-rata untuk mobil kecil $4$ $m^{2}$ dan mobil besar $20$ $m^{2}$. Daya tampung maksimum hanya $200$ kendaraan, biaya parkir mobil kecil $Rp. \ 1.000,00$/jam dan mobil besar $Rp.\ 2.000,00$/jam. Diketahui $x$ menyatakan banyak mobil kecil dan $y$ menyatakan banyak mobil besar yang parkir. Jika dalam satu jam terisi penuh dan tidak ada kendaran yang pergi dan datang, model matematika dari masalah diatas adalah...
$ \begin{align} & (A) \ 4x+20y \le 1.750; \ x+y \ge 200; \ x \le 0; \ y \ge 0 \\ & (B) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \ge 0; \ y \ge 0 \\ & (C) \ 4x+20y \ge 1.750; \ x+y \le 200; \ x \le 0; \ y \ge 0 \\ & (D) \ 4x+20y \ge 1.750; \ x+y \le 200; \ x \ge 0; \ y \le 0 \\ & (E) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \le 0; \ y \le 0 \end{align} $
Model pertidaksamaan matematika pertama yang bisa kita dapatkan adalah $x \ge 0$ dan $y \ge 0$ karena keduanya menyatakan banyaknya mobil kecil dan besar yang terparkir sehingga nilai keduanya tidak mungkin negatif.
Selanjutnya dari yang diketahui pada soal kita dapatkan :
$4x+20y \le 1.750$
$x+y \le 200$
Jadi, jawaban yang TEPAT adalah $(B) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \ge 0; \ y \ge 0 $.
Selanjutnya dari yang diketahui pada soal kita dapatkan :
$4x+20y \le 1.750$
$x+y \le 200$
Jadi, jawaban yang TEPAT adalah $(B) \ 4x+20y \le 1.750; \ x+y \le 200; \ x \ge 0; \ y \ge 0 $.
No. 5 Turunan Fungsi Aljabar
Diketahui $f(x) = 4x^{3} + 2x^{2} – 3x + 2$ dan $f'(x)$ adalah turunan pertama dari $f(x)$. Nilai $f'(2) =$ …
$ \begin{align} & (A) \ 28 \\ & (B) \ 32 \\ & (C) \ 43 \\ & (D) \ 48 \\ & (E) \ 53 \end{align} $
Diketahui $f(x) = 4x^{3} + 2x^{2} – 3x + 2$ dan $f'(x)$ adalah turunan pertama dari $f(x)$. Nilai $f'(2) =$ …
$ \begin{align} & (A) \ 28 \\ & (B) \ 32 \\ & (C) \ 43 \\ & (D) \ 48 \\ & (E) \ 53 \end{align} $
$
\begin{align}
f(x) &= 4x^{3} + 2x^{2} – 3x + 2 \\
f'(x) &= 12x^{2} + 4x – 3 \\
f'(2) &= 12 \left(2^{2} \right) + 4(2) – 3 \\
&= 48 + 8 - 3 \\
&= 53
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 53$.
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ 53$.
No. 6 Operasi Matriks
Diketahui :
$\begin{pmatrix} 2x-1 & 4 \\ 9 & x+y \end{pmatrix}$ $+$ $2 \begin{pmatrix} 3 & -1 \\ -2 & x \end{pmatrix}$ $= \begin{pmatrix} 1 & 2 \\ 5 & 3 \end{pmatrix}$
Tentukan nilai kebenaran dari beberapa pernyataan berikut ini...
HTML Table Generator
Diketahui :
$\begin{pmatrix} 2x-1 & 4 \\ 9 & x+y \end{pmatrix}$ $+$ $2 \begin{pmatrix} 3 & -1 \\ -2 & x \end{pmatrix}$ $= \begin{pmatrix} 1 & 2 \\ 5 & 3 \end{pmatrix}$
Tentukan nilai kebenaran dari beberapa pernyataan berikut ini...
| Pernyataan | Benar | Salah |
|---|---|---|
| $5x+2y=8$ | ||
| $2xy=-36$ | ||
| $6x-3y=-10$ | ||
| $3xy-5=1$ |
$\begin{pmatrix}
2x-1 & 4 \\
9 & x+y
\end{pmatrix}$
$+$
$2 \begin{pmatrix}
3 & -1 \\
-2 & x
\end{pmatrix}$
$= \begin{pmatrix}
1 & 2 \\
5 & 3
\end{pmatrix}$
$\begin{pmatrix} 2x-1 & 4 \\ 9 & x+y \end{pmatrix}$ $+$ $\begin{pmatrix} 6 & -2 \\ -4 & 2x \end{pmatrix}$ $= \begin{pmatrix} 1 & 2 \\ 5 & 3 \end{pmatrix}$
Dengan menggunakan konsep kesamaan matriks kita akan peroleh,
$ \begin{align} 2x-1+6 &= 1 \\ 2x &= -4 \\ x &= -2 \end{align} $
dan
$ \begin{align} x+y+2x &= 3 \\ -2+y+2(-2) &= 3 \\ y &= 9 \end{align} $
Dengan demikian,
(i)
$ \begin{align} 5x+2y &= 5(-2) + 2(9) \\ &= -10+18 \\ &= 8 \ \text{(Benar)} \end{align} $
(ii)
$ \begin{align} 2xy &= 2(-2)(9) \\ &= -36 \ \text{(Benar)} \\ \end{align} $
(iii)
$ \begin{align} 6x-3y &= 6(-2) - 3(9) \\ &= -12 - 27 \\ &= -39 \ \text{(Salah)} \end{align} $
(iv)
$ \begin{align} 3xy-5 &= 3(-2)(9) - 5 \\ &= -54 - 5 \\ &= -59 \ \text{(Salah)} \end{align} $
$\begin{pmatrix} 2x-1 & 4 \\ 9 & x+y \end{pmatrix}$ $+$ $\begin{pmatrix} 6 & -2 \\ -4 & 2x \end{pmatrix}$ $= \begin{pmatrix} 1 & 2 \\ 5 & 3 \end{pmatrix}$
Dengan menggunakan konsep kesamaan matriks kita akan peroleh,
$ \begin{align} 2x-1+6 &= 1 \\ 2x &= -4 \\ x &= -2 \end{align} $
dan
$ \begin{align} x+y+2x &= 3 \\ -2+y+2(-2) &= 3 \\ y &= 9 \end{align} $
Dengan demikian,
(i)
$ \begin{align} 5x+2y &= 5(-2) + 2(9) \\ &= -10+18 \\ &= 8 \ \text{(Benar)} \end{align} $
(ii)
$ \begin{align} 2xy &= 2(-2)(9) \\ &= -36 \ \text{(Benar)} \\ \end{align} $
(iii)
$ \begin{align} 6x-3y &= 6(-2) - 3(9) \\ &= -12 - 27 \\ &= -39 \ \text{(Salah)} \end{align} $
(iv)
$ \begin{align} 3xy-5 &= 3(-2)(9) - 5 \\ &= -54 - 5 \\ &= -59 \ \text{(Salah)} \end{align} $
No. 7 Operasi Matriks
Diketahui matriks :
$A = \begin{pmatrix} 2 & -2 & 3\\ 0 & -3 & 3 \end{pmatrix}$ , $B = \begin{pmatrix} -1 & 1 & 0\\ 2 & -1 & 3 \end{pmatrix}$ dan $C = \begin{pmatrix} 0 & -1 & 1\\ 2 & 1 & 0 \end{pmatrix}$
Jumlah semua elemen matriks hasil dari $A-C+2B=$ ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 7 \\ & (C) \ 8 \\ & (D) \ 11 \\ & (E) \ 12 \end{align} $
Diketahui matriks :
$A = \begin{pmatrix} 2 & -2 & 3\\ 0 & -3 & 3 \end{pmatrix}$ , $B = \begin{pmatrix} -1 & 1 & 0\\ 2 & -1 & 3 \end{pmatrix}$ dan $C = \begin{pmatrix} 0 & -1 & 1\\ 2 & 1 & 0 \end{pmatrix}$
Jumlah semua elemen matriks hasil dari $A-C+2B=$ ...
$ \begin{align} & (A) \ 5 \\ & (B) \ 7 \\ & (C) \ 8 \\ & (D) \ 11 \\ & (E) \ 12 \end{align} $
$=\begin{pmatrix}
2 & -2 & 3\\
0 & -3 & 3
\end{pmatrix}$
$- \begin{pmatrix}
0 & -1 & 1\\
2 & 1 & 0
\end{pmatrix}$
$+ 2 \begin{pmatrix}
-1 & 1 & 0\\
2 & -1 & 3
\end{pmatrix}$
$=\begin{pmatrix} 2 & -2 & 3\\ 0 & -3 & 3 \end{pmatrix}$ $- \begin{pmatrix} 0 & -1 & 1\\ 2 & 1 & 0 \end{pmatrix}$ $+ \begin{pmatrix} -2 & 2 & 0\\ 4 & -2 & 3 \end{pmatrix}$
$= \begin{pmatrix} 0 & 1 & 2\\ 2 & -6 & 9 \end{pmatrix}$
Sehingga jumlah semua elemen matriks hasil dari $A-C+2B$ adalah
$ \begin{align} &= 0+1+2+2+(-6)+9 \\ &=8 \end{align} $
Jadi, jawaban yang TEPAT adalah $(C) \ 8$.
$=\begin{pmatrix} 2 & -2 & 3\\ 0 & -3 & 3 \end{pmatrix}$ $- \begin{pmatrix} 0 & -1 & 1\\ 2 & 1 & 0 \end{pmatrix}$ $+ \begin{pmatrix} -2 & 2 & 0\\ 4 & -2 & 3 \end{pmatrix}$
$= \begin{pmatrix} 0 & 1 & 2\\ 2 & -6 & 9 \end{pmatrix}$
Sehingga jumlah semua elemen matriks hasil dari $A-C+2B$ adalah
$ \begin{align} &= 0+1+2+2+(-6)+9 \\ &=8 \end{align} $
Jadi, jawaban yang TEPAT adalah $(C) \ 8$.
No. 8 Transformasi Geometri
Bayangan titik $A(1,3)$ yang ditranslasi oleh $\begin{pmatrix} -3 \\ 2 \end{pmatrix}$ dan dilanjutkan oleh $\begin{pmatrix} 1 \\ 4 \end{pmatrix}$ adalah...
$ \begin{align} & (A) \ A'(1,9) \\ & (B) \ A'(-1,9) \\ & (C) \ A'(1,-9) \\ & (D) \ A'(-1,-9) \\ & (E) \ A'(9,1) \end{align} $
Bayangan titik $A(1,3)$ yang ditranslasi oleh $\begin{pmatrix} -3 \\ 2 \end{pmatrix}$ dan dilanjutkan oleh $\begin{pmatrix} 1 \\ 4 \end{pmatrix}$ adalah...
$ \begin{align} & (A) \ A'(1,9) \\ & (B) \ A'(-1,9) \\ & (C) \ A'(1,-9) \\ & (D) \ A'(-1,-9) \\ & (E) \ A'(9,1) \end{align} $
$\begin{pmatrix}
x' \\
y'
\end{pmatrix}$
$=\begin{pmatrix}
1 \\
3
\end{pmatrix}$
$+\begin{pmatrix}
-3 \\
2
\end{pmatrix}$
$+\begin{pmatrix}
1 \\
4
\end{pmatrix}$
$\begin{pmatrix} x' \\ y' \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 9 \end{pmatrix}$
Jadi, jawaban yang TEPAT adalah $(B) \ A'(-1,9)$.
$\begin{pmatrix} x' \\ y' \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 9 \end{pmatrix}$
Jadi, jawaban yang TEPAT adalah $(B) \ A'(-1,9)$.
No. 9 Transformasi Geometri
Bayangan garis $y=10-2x$ yang dicerminkan terhadap sumbu-$x$ dilanjutkan dengan pencerminan terhadap sumbu-$y$ adalah...
$ \begin{align} & (A) \ x=10-2y \\ & (B) \ x=10+2y \\ & (C) \ y=10+2x \\ & (D) \ y=-10+2x \\ & (E) \ y=-10-2x \end{align} $
Bayangan garis $y=10-2x$ yang dicerminkan terhadap sumbu-$x$ dilanjutkan dengan pencerminan terhadap sumbu-$y$ adalah...
$ \begin{align} & (A) \ x=10-2y \\ & (B) \ x=10+2y \\ & (C) \ y=10+2x \\ & (D) \ y=-10+2x \\ & (E) \ y=-10-2x \end{align} $
Untuk mengerjakan soal ini kita akan pakai cara kreatif, CARA CEPAT!
$ \begin{align} -y &= 10-2(-x) \\ -y &= 10+2x \\ y &= -10-2x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ y=-10-2x$.
Jika sebuah persamaan dicerminkan terhadap sumbu-$x$ maka variabel $y$ berubah tanda, sebaliknya jika dicerminkan terhadap sumbu-$y$ maka variabel $x$ nya yang berubah tanda.Sehingga karena dicerminkan terhadap sumbu-$x$ dilanjutkan dengan pencerminan terhadap sumbu-$y$ maka bayangan garis $y=10-2x$ akan menjadi,
$ \begin{align} -y &= 10-2(-x) \\ -y &= 10+2x \\ y &= -10-2x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E) \ y=-10-2x$.
No. 10 Statistika
Data berikut merupakan data berat badan balita yang mengikuti kegiatan Posyandu.
Nilai median dari data di atas adalah...
$ \begin{align} & (A) \ 33,55 \\ & (B) \ 35,23 \\ & (C) \ 36,59 \\ & (D) \ 37,59 \\ & (E) \ 37,77 \end{align} $
Data berikut merupakan data berat badan balita yang mengikuti kegiatan Posyandu.
Nilai median dari data di atas adalah...
$ \begin{align} & (A) \ 33,55 \\ & (B) \ 35,23 \\ & (C) \ 36,59 \\ & (D) \ 37,59 \\ & (E) \ 37,77 \end{align} $
Hal pertama yang harus kita cari dalam menghitung nilai median adalah letak kelas median.
Carannya dengan mencari data ke-$\dfrac{1}{2}N = \dfrac{1}{2} \times 40 = 20$.
Dari tabel kita dapatkan bahwa data ke-$20$ masuk pada kelas keempat.
Sehingga nilai mediannya adalah,
$ \begin{align} Me &= T_{b} + \dfrac{\frac{1}{2}N-f_{k}}{f} \ (c) \\ &= 35,5 + \dfrac{20-18}{11} \ (6) \\ &= 35,5 + 1,09 \\ &= 36,59 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 36,59$.
Carannya dengan mencari data ke-$\dfrac{1}{2}N = \dfrac{1}{2} \times 40 = 20$.
Dari tabel kita dapatkan bahwa data ke-$20$ masuk pada kelas keempat.
Sehingga nilai mediannya adalah,
$ \begin{align} Me &= T_{b} + \dfrac{\frac{1}{2}N-f_{k}}{f} \ (c) \\ &= 35,5 + \dfrac{20-18}{11} \ (6) \\ &= 35,5 + 1,09 \\ &= 36,59 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 36,59$.
No. 11 Turunan Fungsi
Turunan pertama dari $y=(2x+5)^6$ adalah $y’=$...
$ \begin{align} & (A) \ 6(2x+5)^5 \\ & (B) \ -6(2x+5)^5 \\ & (C) \ 12(2x+5)^6 \\ & (D) \ -12(2x+5)^6 \\ & (E) \ 12(2x+5)^5 \end{align} $
Turunan pertama dari $y=(2x+5)^6$ adalah $y’=$...
$ \begin{align} & (A) \ 6(2x+5)^5 \\ & (B) \ -6(2x+5)^5 \\ & (C) \ 12(2x+5)^6 \\ & (D) \ -12(2x+5)^6 \\ & (E) \ 12(2x+5)^5 \end{align} $
Gunakan aturan rantai untuk menyelesaikan turunan fungsi $y$.
Sehingga,
$ \begin{align} y &= (2x+5)^6 \\ &= 6(2x+5)^5 (2) \\ &= 12(2x+5)^5 \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ 12(2x+5)^5$.
Sehingga,
$ \begin{align} y &= (2x+5)^6 \\ &= 6(2x+5)^5 (2) \\ &= 12(2x+5)^5 \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ 12(2x+5)^5$.
No. 12 Barisan dan Deret
Suku pertama suatu barisan geometri adalah $64$ dan suku ke–$4$ sama dengan $–8$. Suku ke–$6$ barisan tersebut adalah...
$ \begin{align} & (A) \ -4 \\ & (B) \ -2 \\ & (C) \ 1 \\ & (D) \ 2 \\ & (E) \ 4 \end{align} $
Suku pertama suatu barisan geometri adalah $64$ dan suku ke–$4$ sama dengan $–8$. Suku ke–$6$ barisan tersebut adalah...
$ \begin{align} & (A) \ -4 \\ & (B) \ -2 \\ & (C) \ 1 \\ & (D) \ 2 \\ & (E) \ 4 \end{align} $
Rumus suku ke-$n$ dari Barisan Geometri adalah :
$U_n=ar^{n-1}$
Sehingga,
$ \begin{align} U_4 &= 64 \left(r^{3} \right) \\ -8 &= 64 \left(r^{3} \right) \\ -\dfrac{1}{8} &= r^{3} \\ r &= -\dfrac{1}{2} \end{align} $
Selanjutnya kita akan gunakan nilai $r=-\dfrac{1}{2}$ untuk menghitung nilai dari suku ke-$6$.
$ \begin{align} U_6 &= 64 \left( -\dfrac{1}{2} \right)^5 \\ &= 64 \left( -\dfrac{1}{32} \right) \\ &= -2 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(B) \ -2$.
$U_n=ar^{n-1}$
Sehingga,
$ \begin{align} U_4 &= 64 \left(r^{3} \right) \\ -8 &= 64 \left(r^{3} \right) \\ -\dfrac{1}{8} &= r^{3} \\ r &= -\dfrac{1}{2} \end{align} $
Selanjutnya kita akan gunakan nilai $r=-\dfrac{1}{2}$ untuk menghitung nilai dari suku ke-$6$.
$ \begin{align} U_6 &= 64 \left( -\dfrac{1}{2} \right)^5 \\ &= 64 \left( -\dfrac{1}{32} \right) \\ &= -2 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(B) \ -2$.
No. 13 Barisan dan Deret
Suku ke-$3$ dan suku ke-$10$ suatu barisan aritmatika adalah $-5$ dan $51$. Suku ke–$20$ barisan tersebut adalah...
$ \begin{align} & (A) \ 131 \\ & (B) \ 142 \\ & (C) \ 155 \\ & (D) \ 201 \\ & (E) \ 211 \end{align} $
Suku ke-$3$ dan suku ke-$10$ suatu barisan aritmatika adalah $-5$ dan $51$. Suku ke–$20$ barisan tersebut adalah...
$ \begin{align} & (A) \ 131 \\ & (B) \ 142 \\ & (C) \ 155 \\ & (D) \ 201 \\ & (E) \ 211 \end{align} $
Cara CEPAT!!!
$ \begin{align} b &= \dfrac{U_{10} - U_3}{10-3} \\ &= \dfrac{51-(-5)}{7} \\ &= 8 \end{align} $
Kita peroleh,
$ \begin{align} U_3 &= a+2b \\ -5 &= a+2(8) \\ -5 &= a+16 \\ a &= -21 \end{align} $
Dengan demikian,
$ \begin{align} U_{20} &= a+19b \\ &= -21+19(8) \\ &= -21+152 \\ &= 131 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ 131$.
$ \begin{align} b &= \dfrac{U_{10} - U_3}{10-3} \\ &= \dfrac{51-(-5)}{7} \\ &= 8 \end{align} $
Kita peroleh,
$ \begin{align} U_3 &= a+2b \\ -5 &= a+2(8) \\ -5 &= a+16 \\ a &= -21 \end{align} $
Dengan demikian,
$ \begin{align} U_{20} &= a+19b \\ &= -21+19(8) \\ &= -21+152 \\ &= 131 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ 131$.
No. 14 Barisan dan Deret
Suku ke-$25$ suatu barisan aritmatika $4,7,10,13, \dots$ adalah...
$ \begin{align} & (A) \ 54 \\ & (B) \ 62 \\ & (C) \ 76 \\ & (D) \ 81 \\ & (E) \ 96 \end{align} $
Suku ke-$25$ suatu barisan aritmatika $4,7,10,13, \dots$ adalah...
$ \begin{align} & (A) \ 54 \\ & (B) \ 62 \\ & (C) \ 76 \\ & (D) \ 81 \\ & (E) \ 96 \end{align} $
Dari soal kita dapatkan bahwa $a=4$ dan nilai beda $b=3$.
Sehingga,
$ \begin{align} U_{25} &= a+24b \\ &= 4+24(3) \\ &= 76 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 76$.
Sehingga,
$ \begin{align} U_{25} &= a+24b \\ &= 4+24(3) \\ &= 76 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 76$.
No. 15 Barisan dan Deret
Suku ke-$2$ dan suku ke-$5$ suatu barisan geometri adalah $1$ dan $8$. Suku ke–$11$ barisan tersebut adalah...
$ \begin{align} & (A) \ 128 \\ & (B) \ 256 \\ & (C) \ 512 \\ & (D) \ 1024 \\ & (E) \ 2048 \end{align} $
Suku ke-$2$ dan suku ke-$5$ suatu barisan geometri adalah $1$ dan $8$. Suku ke–$11$ barisan tersebut adalah...
$ \begin{align} & (A) \ 128 \\ & (B) \ 256 \\ & (C) \ 512 \\ & (D) \ 1024 \\ & (E) \ 2048 \end{align} $
Cara CEPAT!!!
$ \begin{align} r &= \sqrt[5-2]{\dfrac{U_5}{U_2}} \\ &= \sqrt[3]{\dfrac{8}{1}} \\ &= 2 \end{align} $
$ \begin{align} U_2 &= ar \\ 1 &= a(2) \\ a &= \dfrac{1}{2} \end{align} $
Sehingga,
$ \begin{align} U_{11} &= ar^{10} \\ &= \dfrac{1}{2} \ \left( 2^{10} \right) \\ &= \dfrac{1}{2} \ (1024) \\ &= 512 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(C) \ 512$.
$ \begin{align} r &= \sqrt[5-2]{\dfrac{U_5}{U_2}} \\ &= \sqrt[3]{\dfrac{8}{1}} \\ &= 2 \end{align} $
$ \begin{align} U_2 &= ar \\ 1 &= a(2) \\ a &= \dfrac{1}{2} \end{align} $
Sehingga,
$ \begin{align} U_{11} &= ar^{10} \\ &= \dfrac{1}{2} \ \left( 2^{10} \right) \\ &= \dfrac{1}{2} \ (1024) \\ &= 512 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(C) \ 512$.
No. 16 Kaidah Pencacahan
Sebuah kelompok yang terdiri dari $7$ orang sedang duduk mengelilingi sebuah meja diskusi yang berbentuk lingkaran. Banyaknya cara agar mereka dapat duduk mengelilingi meja diskusi dengan urutan yang berbeda adalah...
$ \begin{align} & (A) \ 36 \\ & (B) \ 48 \\ & (C) \ 120 \\ & (D) \ 720 \\ & (E) \ 840 \end{align} $
Sebuah kelompok yang terdiri dari $7$ orang sedang duduk mengelilingi sebuah meja diskusi yang berbentuk lingkaran. Banyaknya cara agar mereka dapat duduk mengelilingi meja diskusi dengan urutan yang berbeda adalah...
$ \begin{align} & (A) \ 36 \\ & (B) \ 48 \\ & (C) \ 120 \\ & (D) \ 720 \\ & (E) \ 840 \end{align} $
Permutasi Siklik,
$ \begin{align} P_{siklik} &= (7-1)! \\ &= 6! \\ &= 720 \end{align} $
Jadi. jawaban yang BENAR adalah $(D) \ 720$.
$ \begin{align} P_{siklik} &= (7-1)! \\ &= 6! \\ &= 720 \end{align} $
Jadi. jawaban yang BENAR adalah $(D) \ 720$.
No. 17 Relasi dan Fungsi
Batas - batas nilai $x$ yang merupakan domain dari fungsi $f(x)=\sqrt{x^{2}-5x-6}$ adalah...
$ \begin{align} & (A) \ -2 \le x \le 3 \\ & (B) \ -6 \le x \le 1 \\ & (C) \ -1 \le x \le 6 \\ & (D) \ x \le -2 \ \text{atau} \ x \ge 3 \\ & (E) \ x \le -1 \ \text{atau} \ x \ge 6 \end{align} $
Batas - batas nilai $x$ yang merupakan domain dari fungsi $f(x)=\sqrt{x^{2}-5x-6}$ adalah...
$ \begin{align} & (A) \ -2 \le x \le 3 \\ & (B) \ -6 \le x \le 1 \\ & (C) \ -1 \le x \le 6 \\ & (D) \ x \le -2 \ \text{atau} \ x \ge 3 \\ & (E) \ x \le -1 \ \text{atau} \ x \ge 6 \end{align} $
Domain dari sebuah fungsi irasional $y=\sqrt{g(x)}$ adalah $g(x) \ge 0$.
Sehingga kita akan dapatkan,
$ \begin{align} x^{2}-5x-6 & \ge 0 \\ (x-6)(x+1) & \ge 0 \\ x \le -1 \ \text{atau} \ x & \ge 6 \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ x \le -1 \ \text{atau} \ x \ge 6$.
Sehingga kita akan dapatkan,
$ \begin{align} x^{2}-5x-6 & \ge 0 \\ (x-6)(x+1) & \ge 0 \\ x \le -1 \ \text{atau} \ x & \ge 6 \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ x \le -1 \ \text{atau} \ x \ge 6$.
No. 18 Fungsi Komposisi
Jika $(f \ \circ \ g)(x)=x^{2}+2x-8$ dan $f(x)=2x+2$ maka nilai $g(x)$ yang memenuhi adalah...
$ \begin{align} & (A) \ x^{2}+x-5 \\ & (B) \ \dfrac{1}{2}x^{2}+x-5 \\ & (C) \ 2x^{2}+2x-10 \\ & (D) \ \dfrac{1}{3}x^{2}+2x-5 \\ & (E) \ 3x^{2}+x-5 \end{align} $
Jika $(f \ \circ \ g)(x)=x^{2}+2x-8$ dan $f(x)=2x+2$ maka nilai $g(x)$ yang memenuhi adalah...
$ \begin{align} & (A) \ x^{2}+x-5 \\ & (B) \ \dfrac{1}{2}x^{2}+x-5 \\ & (C) \ 2x^{2}+2x-10 \\ & (D) \ \dfrac{1}{3}x^{2}+2x-5 \\ & (E) \ 3x^{2}+x-5 \end{align} $
$
\begin{align}
(f \ \circ \ g)(x) &= x^{2}+2x-8 \\
f\left( g(x) \right) &= x^{2}+2x-8 \\
2 \ g(x) +2 &= x^{2}+2x-8 \\
2 \ g(x) &= x^{2}+2x-10 \\
g(x) &= \dfrac{1}{2}x^{2}+x-5
\end{align}
$
Jadi, jawaban yang TEPAT adalah $(B) \ \dfrac{1}{2}x^{2}+x-5 $.
Jadi, jawaban yang TEPAT adalah $(B) \ \dfrac{1}{2}x^{2}+x-5 $.
No. 19 Fungsi Invers
Jika $f(x)=\dfrac{3x+2}{5x-1}$ maka $f^{-1}(x)=$...
$ \begin{align} & (A) \ \dfrac{3x+2}{5x-3} \\ & (B) \ \dfrac{-x+2}{5x-3} \\ & (C) \ \dfrac{x+2}{5x+3} \\ & (D) \ \dfrac{x+2}{-5x+3} \\ & (E) \ \dfrac{x+2}{5x-3} \end{align} $
Jika $f(x)=\dfrac{3x+2}{5x-1}$ maka $f^{-1}(x)=$...
$ \begin{align} & (A) \ \dfrac{3x+2}{5x-3} \\ & (B) \ \dfrac{-x+2}{5x-3} \\ & (C) \ \dfrac{x+2}{5x+3} \\ & (D) \ \dfrac{x+2}{-5x+3} \\ & (E) \ \dfrac{x+2}{5x-3} \end{align} $
Cara CEPAT!!!
Jika $f(x)=\dfrac{ax+b}{cx+d}$ $\to$ $f^{-1}(x)=\dfrac{-dx+b}{cx-a}$.
Sehingga,
$f(x)=\dfrac{3x+2}{5x-1}$ $\to$ $f^{-1}(x)=\dfrac{x+2}{5x-3}$.
Jadi, pilihan jawaban yang BENAR adalah $(E) \ \dfrac{x+2}{5x-3}$.
Jika $f(x)=\dfrac{ax+b}{cx+d}$ $\to$ $f^{-1}(x)=\dfrac{-dx+b}{cx-a}$.
Sehingga,
$f(x)=\dfrac{3x+2}{5x-1}$ $\to$ $f^{-1}(x)=\dfrac{x+2}{5x-3}$.
Jadi, pilihan jawaban yang BENAR adalah $(E) \ \dfrac{x+2}{5x-3}$.
No. 20 Dimensi Tiga
Jika panjang diagonal sisi sebuah kubus adalah $6$ $cm$, maka luas bidang diagonal kubus tersebut adalah... $cm^{2}$
$ \begin{align} & (A) \ 21\sqrt{3} \\ & (B) \ 18 \\ & (C) \ 18\sqrt{2} \\ & (D) \ 15 \\ & (E) \ 12\sqrt{2} \end{align} $
Jika panjang diagonal sisi sebuah kubus adalah $6$ $cm$, maka luas bidang diagonal kubus tersebut adalah... $cm^{2}$
$ \begin{align} & (A) \ 21\sqrt{3} \\ & (B) \ 18 \\ & (C) \ 18\sqrt{2} \\ & (D) \ 15 \\ & (E) \ 12\sqrt{2} \end{align} $
Jika kubus mempunyai panjang rusuk $a$ maka panjang diagonal sisi kubus adalah $a\sqrt{2}$.
Sehingga,
$ \begin{align} a\sqrt{2} &= 6 \\ a &= \dfrac{6}{\sqrt{2}} \end{align} $
Luas bidang diagonal kubus,
$ \begin{align} L &= a^{2}\sqrt{2} \\ &= \left(\dfrac{6}{\sqrt{2}} \right)^{2} \sqrt{2} \\ &= \left( \dfrac{36}{2} \right) \sqrt{2} \\ &= 18\sqrt{2} \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(C) \ 18\sqrt{2}$.
Sehingga,
$ \begin{align} a\sqrt{2} &= 6 \\ a &= \dfrac{6}{\sqrt{2}} \end{align} $
Luas bidang diagonal kubus,
$ \begin{align} L &= a^{2}\sqrt{2} \\ &= \left(\dfrac{6}{\sqrt{2}} \right)^{2} \sqrt{2} \\ &= \left( \dfrac{36}{2} \right) \sqrt{2} \\ &= 18\sqrt{2} \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(C) \ 18\sqrt{2}$.
No. 21 Peluang Kejadian
Dua buah dadu dilempar sebanyak $144$ kali. Frekuensi harapan kejadian munculnya mata dadu berjumlah $8$ adalah...
$ \begin{align} & (A) \ 10 \\ & (B) \ 15 \\ & (C) \ 18 \\ & (D) \ 20 \\ & (E) \ 25 \end{align} $
Dua buah dadu dilempar sebanyak $144$ kali. Frekuensi harapan kejadian munculnya mata dadu berjumlah $8$ adalah...
$ \begin{align} & (A) \ 10 \\ & (B) \ 15 \\ & (C) \ 18 \\ & (D) \ 20 \\ & (E) \ 25 \end{align} $
Banyak kejadian muncul mata dadu berjumlah $8$ $\to$ $\{ (6,2),(5,3),(4,4),(3,5),(2,6) \}$, $n(A)=5$
Ruang sampel dua dadu $\to$ $n(S)=6^{2}$
Sehingga peluang munculnya dua mata dadu berjumlah $8$,
$ \begin{align} P(A) &= \dfrac{n(A)}{n(S)} \\ &= \dfrac{5}{6^{2}} \\ &= \dfrac{5}{36} \end{align} $
Dengan demikian nilai frekuansi harapannya,
$ \begin{align} FH &= n \times P(A) \\ &= 144 \times \dfrac{5}{36} \\ &= 20 \end{align} $
Jadi, jawaban yang TEPAT adalah $(D) \ 20$.
Ruang sampel dua dadu $\to$ $n(S)=6^{2}$
Sehingga peluang munculnya dua mata dadu berjumlah $8$,
$ \begin{align} P(A) &= \dfrac{n(A)}{n(S)} \\ &= \dfrac{5}{6^{2}} \\ &= \dfrac{5}{36} \end{align} $
Dengan demikian nilai frekuansi harapannya,
$ \begin{align} FH &= n \times P(A) \\ &= 144 \times \dfrac{5}{36} \\ &= 20 \end{align} $
Jadi, jawaban yang TEPAT adalah $(D) \ 20$.
No. 22 Fungsi Komposisi dan Invers
Jika diketahui $f(x)=2x-3$ dan $g(x)=x^{2}+4x+7$ maka :
(1) $f^{-1}(0)=(2)$
(2) $(g \ \circ \ f)(0)=4$
(3) $\left( \dfrac{f}{g} \right)(1)=1$
(4) $f^{-1}(x)=\dfrac{x+3}{2}$
Jawaban yang TEPAT untuk persoalan di atas adalah...
$ \begin{align} & (A) \ (1), \ (2) \ \text{dan} \ (3) \ \text{benar}. \\ & (B) \ (1) \ \text{dan} \ (3) \ \text{benar}. \\ & (C) \ (2) \ \text{dan} \ (4) \ \text{benar}. \\ & (D) \ (4) \ \text{saja benar}. \\ & (E) \ \text{Semua benar.} \end{align} $
Jika diketahui $f(x)=2x-3$ dan $g(x)=x^{2}+4x+7$ maka :
(1) $f^{-1}(0)=(2)$
(2) $(g \ \circ \ f)(0)=4$
(3) $\left( \dfrac{f}{g} \right)(1)=1$
(4) $f^{-1}(x)=\dfrac{x+3}{2}$
Jawaban yang TEPAT untuk persoalan di atas adalah...
$ \begin{align} & (A) \ (1), \ (2) \ \text{dan} \ (3) \ \text{benar}. \\ & (B) \ (1) \ \text{dan} \ (3) \ \text{benar}. \\ & (C) \ (2) \ \text{dan} \ (4) \ \text{benar}. \\ & (D) \ (4) \ \text{saja benar}. \\ & (E) \ \text{Semua benar.} \end{align} $
Pernyataan (1)
Ingat kembali definisi dari fungsi invers, yaitu : $f(a)=b$ jika dan hanya jika $f^{-1}(b)=a$.
Sehingga $f^{-1}(0)=(2)$ jika dan hanya jika $f(2)=0$.
$f(2)=2(2)-3 \ne 0$.
Pernyataan (1) bernilai salah.
Pernyataan (2)
$ \begin{align} (g \circ f)(x) &= (2x-3)^{2}+4(2x-3)+7 \\ (g \circ f)(0) &= (2(0)-3)^{2}+4(2(0)-3)+7 \\ &= (-3)^{2}+4(-3)+7 \\ &= 9-12+7 \\ &= 4 \end{align} $
Pernyataan (2) bernilai benar.
Pernyataan (3)
$ \begin{align} \left( \dfrac{f}{g} \right)(x) &= \dfrac{2x-3}{x^{2}+4x+7} \\ \left( \dfrac{f}{g} \right)(1) &= \dfrac{2(1)-3}{(1)^{2}+4(1)+7} \\ &= \dfrac{-1}{1+4+7} \\ &= -\dfrac{1}{12} \end{align} $
Pernyataan (3) bernilai salah.
Pernyataan (4)
Untuk mencari invers dari sebuah fungsi maka ada tiga langkah yang bisa kita lakukan :
$ \begin{align} f(x) &= 2x-3 \\ y &= 2x-3 \\ y+3 &= 2x \\ x &= \dfrac{y+3}{2} \\ f^{-1}(x) &= \dfrac{x+3}{2} \end{align} $
Pernyataan (4) bernilai benar.
Jadi, jawaban yang TEPAT adalah $(C) \ (2) \ \text{dan} \ (4) \ \text{benar}.$
Ingat kembali definisi dari fungsi invers, yaitu : $f(a)=b$ jika dan hanya jika $f^{-1}(b)=a$.
Sehingga $f^{-1}(0)=(2)$ jika dan hanya jika $f(2)=0$.
$f(2)=2(2)-3 \ne 0$.
Pernyataan (1) bernilai salah.
Pernyataan (2)
$ \begin{align} (g \circ f)(x) &= (2x-3)^{2}+4(2x-3)+7 \\ (g \circ f)(0) &= (2(0)-3)^{2}+4(2(0)-3)+7 \\ &= (-3)^{2}+4(-3)+7 \\ &= 9-12+7 \\ &= 4 \end{align} $
Pernyataan (2) bernilai benar.
Pernyataan (3)
$ \begin{align} \left( \dfrac{f}{g} \right)(x) &= \dfrac{2x-3}{x^{2}+4x+7} \\ \left( \dfrac{f}{g} \right)(1) &= \dfrac{2(1)-3}{(1)^{2}+4(1)+7} \\ &= \dfrac{-1}{1+4+7} \\ &= -\dfrac{1}{12} \end{align} $
Pernyataan (3) bernilai salah.
Pernyataan (4)
Untuk mencari invers dari sebuah fungsi maka ada tiga langkah yang bisa kita lakukan :
- Misalkan $f(x)$ menjadi y.
- Sederhanakan fungsinya hingga mendapatkan nilai dari $x$ nya.
- Fungsi invers didapatkan dengan mengganti variabel $y$ menjadi variabel $x$.
$ \begin{align} f(x) &= 2x-3 \\ y &= 2x-3 \\ y+3 &= 2x \\ x &= \dfrac{y+3}{2} \\ f^{-1}(x) &= \dfrac{x+3}{2} \end{align} $
Pernyataan (4) bernilai benar.
Jadi, jawaban yang TEPAT adalah $(C) \ (2) \ \text{dan} \ (4) \ \text{benar}.$
No. 23 Peluang Kejadian
Sebuah kotak berisi $12$ bola lampu yang dijual pada sebuah toko "BINTANG TERANG". Dari $12$ bola lampu yang ada pemilik toko baru menyadari bahwa ternyata ada $2$ lampu yang rusak. Jika hari itu terdapat tiga orang pembeli maka peluang pembeli ketiga mendapatkan bola lampu yang rusak adalah...
$ \begin{align} & (A) \ \dfrac{1}{6} \\ & (B) \ \dfrac{1}{3} \\ & (C) \ \dfrac{3}{12} \\ & (D) \ \dfrac{7}{12} \\ & (E) \ \dfrac{5}{12} \end{align} $
Sebuah kotak berisi $12$ bola lampu yang dijual pada sebuah toko "BINTANG TERANG". Dari $12$ bola lampu yang ada pemilik toko baru menyadari bahwa ternyata ada $2$ lampu yang rusak. Jika hari itu terdapat tiga orang pembeli maka peluang pembeli ketiga mendapatkan bola lampu yang rusak adalah...
$ \begin{align} & (A) \ \dfrac{1}{6} \\ & (B) \ \dfrac{1}{3} \\ & (C) \ \dfrac{3}{12} \\ & (D) \ \dfrac{7}{12} \\ & (E) \ \dfrac{5}{12} \end{align} $
Konteks dalam cerita masuk dalam kejadian pengambilan tanpa pengembalian.
Karena pembeli ketiga mendapatkan bola lampu yang rusak maka kejadiannya ada tiga kemungkinan yaitu : (Baik, Baik, Rusak), (Baik, Rusak, Rusak) dan (Rusak, Baik, Rusak).
Sehingga,
$ \begin{align} P(\text{Baik},\text{Baik},\text{Rusak}) &= \dfrac{10}{12} \times \dfrac{9}{11} \times \dfrac{2}{10} \\ &= \dfrac{9}{66} \end{align} $
$ \begin{align} P(\text{Baik},\text{Rusak},\text{Rusak}) &= \dfrac{10}{12} \times \dfrac{2}{11} \times \dfrac{1}{10} \\ &= \dfrac{1}{66} \end{align} $
$ \begin{align} P(\text{Rusak},\text{Baik},\text{Rusak}) &= \dfrac{2}{12} \times \dfrac{10}{11} \times \dfrac{1}{10} \\ &= \dfrac{1}{66} \end{align} $
Dengan demikian peluang total dari kejadian pembeli ketiga mendapatkan bola lampu yang rusak adalah :
$ \begin{align} &= \dfrac{9}{66} + \dfrac{1}{66} + \dfrac{1}{66} \\ &= \dfrac{11}{66} = \dfrac{1}{6} \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ \dfrac{1}{6}$.
Karena pembeli ketiga mendapatkan bola lampu yang rusak maka kejadiannya ada tiga kemungkinan yaitu : (Baik, Baik, Rusak), (Baik, Rusak, Rusak) dan (Rusak, Baik, Rusak).
Sehingga,
$ \begin{align} P(\text{Baik},\text{Baik},\text{Rusak}) &= \dfrac{10}{12} \times \dfrac{9}{11} \times \dfrac{2}{10} \\ &= \dfrac{9}{66} \end{align} $
$ \begin{align} P(\text{Baik},\text{Rusak},\text{Rusak}) &= \dfrac{10}{12} \times \dfrac{2}{11} \times \dfrac{1}{10} \\ &= \dfrac{1}{66} \end{align} $
$ \begin{align} P(\text{Rusak},\text{Baik},\text{Rusak}) &= \dfrac{2}{12} \times \dfrac{10}{11} \times \dfrac{1}{10} \\ &= \dfrac{1}{66} \end{align} $
Dengan demikian peluang total dari kejadian pembeli ketiga mendapatkan bola lampu yang rusak adalah :
$ \begin{align} &= \dfrac{9}{66} + \dfrac{1}{66} + \dfrac{1}{66} \\ &= \dfrac{11}{66} = \dfrac{1}{6} \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ \dfrac{1}{6}$.
No. 24 Fungsi Kuadrat
Perhatikan gambar berikut!
Persamaan fungsi kuadrat yang sesuai dengan grafik kurva di atas adalah...
$ \begin{align} & (A) \ y=3-2x-2x^{2} \\ & (B) \ y=3+2x-2x^{2} \\ & (C) \ y=3+2x-x^{2} \\ & (D) \ y=x^{2}+2x-3 \\ & (E) \ y=2x^{2}-2x-3 \end{align} $
Perhatikan gambar berikut!
Persamaan fungsi kuadrat yang sesuai dengan grafik kurva di atas adalah...
$ \begin{align} & (A) \ y=3-2x-2x^{2} \\ & (B) \ y=3+2x-2x^{2} \\ & (C) \ y=3+2x-x^{2} \\ & (D) \ y=x^{2}+2x-3 \\ & (E) \ y=2x^{2}-2x-3 \end{align} $
Karena kurva memotong sumbu-$x$ di $(-1,0)$ dan $(3,0)$ maka,
$ \begin{align} y &= a(x-x_1)(x-x_2) \\ y &= a(x+1)(x-3) \\ \end{align} $
Kurva juga melalui titik $(2,3)$ yang artinya,
$ \begin{align} 3 &= a(2+1)(2-3) \\ 3 &= a(-3) \\ a &= -1 \end{align} $
Dengan demikian kita akan peroleh fungsi kuadratnya,
$ \begin{align} y &= a(x+1)(x-3) \\ y &= (-1)(x^{2}-2x-3) \\ y &= 3+2x-x^{2} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ y=3+2x-x^{2}$.
$ \begin{align} y &= a(x-x_1)(x-x_2) \\ y &= a(x+1)(x-3) \\ \end{align} $
Kurva juga melalui titik $(2,3)$ yang artinya,
$ \begin{align} 3 &= a(2+1)(2-3) \\ 3 &= a(-3) \\ a &= -1 \end{align} $
Dengan demikian kita akan peroleh fungsi kuadratnya,
$ \begin{align} y &= a(x+1)(x-3) \\ y &= (-1)(x^{2}-2x-3) \\ y &= 3+2x-x^{2} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ y=3+2x-x^{2}$.
No. 25 Vektor
Jika $\vec{a}= 3\vec{i}-\vec{j}+6\vec{k}$ dan $\vec{b}= 4\vec{i}+2\vec{j}-5\vec{k}$ maka panjang proyeksi skalar $\vec{a}$ pada $\vec{b}$ adalah...
$ \begin{align} & (A) \ \dfrac{20}{2\sqrt{5}} \\ & (B) \ \dfrac{10}{2\sqrt{5}} \\ & (C) \ \dfrac{20}{5\sqrt{3}} \\ & (D) \ \dfrac{20}{2\sqrt{5}} \\ & (E) \ \dfrac{20}{3\sqrt{5}} \end{align} $
Jika $\vec{a}= 3\vec{i}-\vec{j}+6\vec{k}$ dan $\vec{b}= 4\vec{i}+2\vec{j}-5\vec{k}$ maka panjang proyeksi skalar $\vec{a}$ pada $\vec{b}$ adalah...
$ \begin{align} & (A) \ \dfrac{20}{2\sqrt{5}} \\ & (B) \ \dfrac{10}{2\sqrt{5}} \\ & (C) \ \dfrac{20}{5\sqrt{3}} \\ & (D) \ \dfrac{20}{2\sqrt{5}} \\ & (E) \ \dfrac{20}{3\sqrt{5}} \end{align} $
Panjang proyeksi skalar dari $\vec{a}$ pada $\vec{b}$,
$ \begin{align} &= \left| \dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \right| \\ &= \left| \dfrac{(3)(4)+(-1)(2)+(6)(-5)}{\sqrt{4^{2}+2^{2}+(-5)^{2}}} \right| \\ &= \left| \dfrac{-20}{\sqrt{45}} \right| \\ &= \dfrac{20}{3\sqrt{5}} \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ \dfrac{20}{3\sqrt{5}}$.
$ \begin{align} &= \left| \dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \right| \\ &= \left| \dfrac{(3)(4)+(-1)(2)+(6)(-5)}{\sqrt{4^{2}+2^{2}+(-5)^{2}}} \right| \\ &= \left| \dfrac{-20}{\sqrt{45}} \right| \\ &= \dfrac{20}{3\sqrt{5}} \end{align} $
Jadi, jawaban yang TEPAT adalah $(E) \ \dfrac{20}{3\sqrt{5}}$.
No. 26 Logaritma
Jika $\log{2}=0,3010$; $\log{3}=0,4771$; dan $\log{7}=0,8451$
maka nilai dari $\log{\sqrt[3]{12}}$ adalah...
$ \begin{align} & (A) \ 0,9357 \\ & (B) \ 0,7395 \\ & (C) \ 0,5973 \\ & (D) \ 0,5397 \\ & (E) \ 0,3597 \end{align} $
Jika $\log{2}=0,3010$; $\log{3}=0,4771$; dan $\log{7}=0,8451$
maka nilai dari $\log{\sqrt[3]{12}}$ adalah...
$ \begin{align} & (A) \ 0,9357 \\ & (B) \ 0,7395 \\ & (C) \ 0,5973 \\ & (D) \ 0,5397 \\ & (E) \ 0,3597 \end{align} $
$
\begin{align}
\log{\sqrt[3]{12}} &= \log{12^{\frac{1}{3}}} \\
&= \log{(2^{2} \times 3)^{\frac{1}{3}}} \\
&= \dfrac{1}{3} \left( \log{2^{2}} + \log{3} \right) \\
&= \dfrac{1}{3} \left( 2\log{2} + \log{3} \right) \\
&= \dfrac{2(0,3010)+0,4771}{3} \\
&= 0,3597
\end{align}
$
Jadi, jawaban yang TEPAT adalah $(E) \ 0,3597$.
Jadi, jawaban yang TEPAT adalah $(E) \ 0,3597$.
No. 27 Logaritma
Jika $\log{\dfrac{a^{2}}{b^{2}}}=12$ maka nilai dari $\log{\sqrt[3]{\dfrac{b}{a}}}$ adalah...
$ \begin{align} & (A) \ -2 \\ & (B) \ -1 \\ & (C) \ 0 \\ & (D) \ 1 \\ & (E) \ 2 \end{align} $
Jika $\log{\dfrac{a^{2}}{b^{2}}}=12$ maka nilai dari $\log{\sqrt[3]{\dfrac{b}{a}}}$ adalah...
$ \begin{align} & (A) \ -2 \\ & (B) \ -1 \\ & (C) \ 0 \\ & (D) \ 1 \\ & (E) \ 2 \end{align} $
Diketahui dalam soal,
$ \begin{align} \log{\dfrac{a^{2}}{b^{2}}} &= 12 \\ \log{\left( \dfrac{a}{b} \right)^{2}} &= 12 \\ 2 \ \log{\dfrac{a}{b}} &= 12 \\ \log{\dfrac{a}{b}} &= 6 \end{align} $
Dengan demikian,
$ \begin{align} \log{\sqrt[3]{\dfrac{b}{a}}} &= \log{\left( \dfrac{b}{a} \right)^{\frac{1}{3}}} \\ &= \dfrac{1}{3} \left( - \log{\dfrac{a}{b}} \right) \\ &= \dfrac{1}{3} \times (-6) \\ &= -2 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ -2$.
$ \begin{align} \log{\dfrac{a^{2}}{b^{2}}} &= 12 \\ \log{\left( \dfrac{a}{b} \right)^{2}} &= 12 \\ 2 \ \log{\dfrac{a}{b}} &= 12 \\ \log{\dfrac{a}{b}} &= 6 \end{align} $
Dengan demikian,
$ \begin{align} \log{\sqrt[3]{\dfrac{b}{a}}} &= \log{\left( \dfrac{b}{a} \right)^{\frac{1}{3}}} \\ &= \dfrac{1}{3} \left( - \log{\dfrac{a}{b}} \right) \\ &= \dfrac{1}{3} \times (-6) \\ &= -2 \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A) \ -2$.
No. 28 Persamaan Eksponen
Nilai $x$ yang memenuhi persamaan eksponen $\sqrt{3^{x-2}}=\dfrac{9^{x-5}}{3^{2x+2}}$ adalah...
$ \begin{align} & (A) \ -22 \\ & (B) \ -18 \\ & (C) \ 10 \\ & (D) \ 9 \\ & (E) \ 3 \end{align} $
Nilai $x$ yang memenuhi persamaan eksponen $\sqrt{3^{x-2}}=\dfrac{9^{x-5}}{3^{2x+2}}$ adalah...
$ \begin{align} & (A) \ -22 \\ & (B) \ -18 \\ & (C) \ 10 \\ & (D) \ 9 \\ & (E) \ 3 \end{align} $
$
\begin{align}
\sqrt{3^{x-2}} &= \dfrac{9^{x-5}}{3^{2x+2}} \\
3^{\left( \frac{x-2}{2} \right)} &= \dfrac{3^{2x-10}}{3^{2x+2}} \\
3^{\left( \frac{x-2}{2} \right)} &= 3^{2x-10-(2x+2)} \\
\hline \\
\dfrac{x-2}{2} &= 2x-10-(2x+2) \\
\dfrac{x-2}{2} &= -12 \\
x-2 &= -24 \\
x &= -22
\end{align}
$
Jadi, jawaban yang TEPAT adalah $(A) \ -22$.
Jadi, jawaban yang TEPAT adalah $(A) \ -22$.
No. 29 Pertidaksamaan Eksponen
Jika $\left( \dfrac{1}{3} \right)^{3x-1} \le 9^{x^{2}+3x-2}$ maka batas - batas nilai $x$ yang memenuhi adalah...
$ \begin{align} & (A) \ -5 \le x \le \dfrac{1}{2} \\ & (B) \ -5 \le x \le \dfrac{1}{2} \\ & (C) \ -\dfrac{1}{2} \le x \le 5 \\ & (D) \ x \le -5 \ \text{atau} \ x \ge \dfrac{1}{2} \\ & (E) \ x \le -\dfrac{1}{2} \ \text{atau} \ x \ge 5 \end{align} $
Jika $\left( \dfrac{1}{3} \right)^{3x-1} \le 9^{x^{2}+3x-2}$ maka batas - batas nilai $x$ yang memenuhi adalah...
$ \begin{align} & (A) \ -5 \le x \le \dfrac{1}{2} \\ & (B) \ -5 \le x \le \dfrac{1}{2} \\ & (C) \ -\dfrac{1}{2} \le x \le 5 \\ & (D) \ x \le -5 \ \text{atau} \ x \ge \dfrac{1}{2} \\ & (E) \ x \le -\dfrac{1}{2} \ \text{atau} \ x \ge 5 \end{align} $
$
\begin{align}
\left( \dfrac{1}{3} \right)^{3x-1} & \le 9^{x^{2}+3x-2} \\
3^{1-3x} & \le 9^{x^{2}+3x-2} \\
3^{1-3x} & \le 3^{2x^{2}+6x-4} \\ \\
\text{Sehingga,} \\
1-3x & \le 2x^{2}+6x-4 \\
0 & \le 2x^{2}+9x-5 \\
0 & \le (2x-1)(x+5) \\
x & \le -5 \ \text{atau} \ x \ge \dfrac{1}{2}
\end{align}
$
Jadi, jawaban yang TEPAT adalah $(D) \ x \le -5 \ \text{atau} \ x \ge \dfrac{1}{2}$.
Jadi, jawaban yang TEPAT adalah $(D) \ x \le -5 \ \text{atau} \ x \ge \dfrac{1}{2}$.
No. 30 Integral Tak Tentu
Hasil dari $\int \sqrt{x+\dfrac{9}{x}-6}\ dx$ adalah...
$ \begin{align} & (A) \ 4\sqrt{x^{3}}-2\sqrt{x}+ c \\ & (B) \ \frac{2}{3}\sqrt{x^{3}}-\frac{5}{2}\sqrt{x^{3}}+ c \\ & (C) \ \frac{2}{3}\sqrt{x^{3}}-6\sqrt{x}+ c \\ & (D) \ 2\sqrt{x^{5}}-\frac{5}{3}\sqrt{x}+ c \\ & (E) \ \frac{5}{2}\sqrt{x^{3}}-4\sqrt{x}+ c \end{align} $
Hasil dari $\int \sqrt{x+\dfrac{9}{x}-6}\ dx$ adalah...
$ \begin{align} & (A) \ 4\sqrt{x^{3}}-2\sqrt{x}+ c \\ & (B) \ \frac{2}{3}\sqrt{x^{3}}-\frac{5}{2}\sqrt{x^{3}}+ c \\ & (C) \ \frac{2}{3}\sqrt{x^{3}}-6\sqrt{x}+ c \\ & (D) \ 2\sqrt{x^{5}}-\frac{5}{3}\sqrt{x}+ c \\ & (E) \ \frac{5}{2}\sqrt{x^{3}}-4\sqrt{x}+ c \end{align} $
$
\begin{align}
& \int \sqrt{x+\dfrac{9}{x}-6}\ dx\\
&= \int \sqrt{ \dfrac{x^{2}+9-6x}{x}}\ dx\\
&= \int \sqrt{ \dfrac{\left(x-3\right)^{2}}{x}}\ dx\\
&= \int \dfrac{x-3}{\sqrt{x}}\ dx\\
&= \int \left(x^{\frac{1}{2}}-3x^{-\frac{1}{2}} \right)\ dx\\
&= \frac{1}{\frac{1}{2}+1} \cdot x^{\frac{1}{2}+1}- \frac{3}{-\frac{1}{2}+1}x^{ -\frac{1}{2}+1} +c \\
&= \frac{1}{\frac{3}{2}} \cdot x^{\frac{3}{2}}- \frac{3}{ \frac{1}{2} }x^{ \frac{1}{2} } +c \\
&= \frac{2}{3} \sqrt{x^{3}}- 6 \sqrt{x} +c
\end{align}
$
Jadi, jawaban yang BENAR adalah $(C) \ \frac{2}{3}\sqrt{x^{3}}-6\sqrt{x}+ c$.
Jadi, jawaban yang BENAR adalah $(C) \ \frac{2}{3}\sqrt{x^{3}}-6\sqrt{x}+ c$.
No. 31 Integral Luas
Luas daerah yang dibatasi kurva $y=x^{2}$ dan $y=2-x$ adalah...
$ \begin{align} & (A) \ 10 \\ & (B) \ \dfrac{9}{2} \\ & (C) \ \dfrac{8}{3} \\ & (D) \ 6 \\ & (E) \ \dfrac{5}{3} \end{align} $
Luas daerah yang dibatasi kurva $y=x^{2}$ dan $y=2-x$ adalah...
$ \begin{align} & (A) \ 10 \\ & (B) \ \dfrac{9}{2} \\ & (C) \ \dfrac{8}{3} \\ & (D) \ 6 \\ & (E) \ \dfrac{5}{3} \end{align} $
Karena hanya dibatasi oleh dua kurva tanpa syarat apapun yang lain, maka kita bisa pakai CARA CEPAT!!!.
$L=\dfrac{D\sqrt{D}}{6a^{2}}$
dimana $D=b^{2}-4ac$
Langkah pertama kita cari $y_1=y_2$,
$ \begin{align} y_1 &= y_2 \\ x^{2} &= 2-x \\ x^{2} &+x-2 = 0 \end{align} $
Sehingga,
$ \begin{align} D &= 1^{2}-4(1)(-2) \\ &= 9 \end{align} $
Dengan demikian,
$ \begin{align} L &= \dfrac{D\sqrt{D}}{6a^{2}} \\ &= \dfrac{9\sqrt{9}}{6 \left( 1^{2} \right)} \\ &= \dfrac{9}{2} \ \text{satuan luas} \end{align} $
Jadi, jawaban yang TEPAT adalah $(B) \ \dfrac{9}{2}$.
$L=\dfrac{D\sqrt{D}}{6a^{2}}$
dimana $D=b^{2}-4ac$
Langkah pertama kita cari $y_1=y_2$,
$ \begin{align} y_1 &= y_2 \\ x^{2} &= 2-x \\ x^{2} &+x-2 = 0 \end{align} $
Sehingga,
$ \begin{align} D &= 1^{2}-4(1)(-2) \\ &= 9 \end{align} $
Dengan demikian,
$ \begin{align} L &= \dfrac{D\sqrt{D}}{6a^{2}} \\ &= \dfrac{9\sqrt{9}}{6 \left( 1^{2} \right)} \\ &= \dfrac{9}{2} \ \text{satuan luas} \end{align} $
Jadi, jawaban yang TEPAT adalah $(B) \ \dfrac{9}{2}$.
No. 32 Program Linear
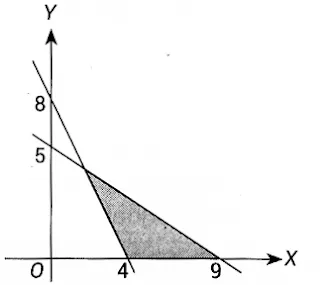
Perhatikan gambar berikut ini!
Sistem pertidaksamaan linear yang sesuai dengan himpunan penyelesaian pada daerah diraster adalah...
$ \begin{align} & (A) \ 5x+9y \le 45 ; \ 2x+y \le 8 ; \ x \ge 0; \ y \ge 0 \\ & (B) \ 5x+9y \le 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0 \\ & (C) \ 5x+9y \ge 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0 \\ & (D) \ 5x+9y \ge 45 ; \ 2x+y \le 8 ; \ x \ge 0; \ y \ge 0 \\ & (E) \ 9x+5y \ge 45 ; \ x+2y \le 8 ; \ x \ge 0; \ y \ge 0 \end{align} $
Perhatikan gambar berikut ini!
Sistem pertidaksamaan linear yang sesuai dengan himpunan penyelesaian pada daerah diraster adalah...
$ \begin{align} & (A) \ 5x+9y \le 45 ; \ 2x+y \le 8 ; \ x \ge 0; \ y \ge 0 \\ & (B) \ 5x+9y \le 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0 \\ & (C) \ 5x+9y \ge 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0 \\ & (D) \ 5x+9y \ge 45 ; \ 2x+y \le 8 ; \ x \ge 0; \ y \ge 0 \\ & (E) \ 9x+5y \ge 45 ; \ x+2y \le 8 ; \ x \ge 0; \ y \ge 0 \end{align} $
Pertama yang kita perhatikan adalah karena daerah hasil (daerah arsir) terletak pada kuadran pertama maka $x \ge 0$ dan $y \ge 0$.
Kita gunakan uji titik dengan menggunakan titik $O(0,0)$ ke dalam sistem pertidaksamaan linearnya.
Sehingga,
(i) $5x+9y \ \cdots \ 45$
Uji $O(0,0)$ maka $0 \ \cdots \ 45$
Karena $O(0,0)$ masuk daerah arsiran maka tanda pertidaksamaannya harus bernilai benar.
Dengan demikian $0 \le 45$
$5x+9y \le 45$
(ii) $8x+4y \ \cdots \ 32$
Uji $O(0,0)$ maka $0 \ \cdots \ 32$
Karena $O(0,0)$ tidak masuk daerah arsiran maka tanda pertidaksamaannya harus bernilai salah.
Dengan demikian $0 \ge 32$
$8x+4y \ge 32$
$2x+y \ge 8$
Jadi, jawaban yang TEPAT adalah $(B) \ 5x+9y \le 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0$.
Kita gunakan uji titik dengan menggunakan titik $O(0,0)$ ke dalam sistem pertidaksamaan linearnya.
Sehingga,
(i) $5x+9y \ \cdots \ 45$
Uji $O(0,0)$ maka $0 \ \cdots \ 45$
Karena $O(0,0)$ masuk daerah arsiran maka tanda pertidaksamaannya harus bernilai benar.
Dengan demikian $0 \le 45$
$5x+9y \le 45$
(ii) $8x+4y \ \cdots \ 32$
Uji $O(0,0)$ maka $0 \ \cdots \ 32$
Karena $O(0,0)$ tidak masuk daerah arsiran maka tanda pertidaksamaannya harus bernilai salah.
Dengan demikian $0 \ge 32$
$8x+4y \ge 32$
$2x+y \ge 8$
Jadi, jawaban yang TEPAT adalah $(B) \ 5x+9y \le 45 ; \ 2x+y \ge 8 ; \ x \ge 0; \ y \ge 0$.
No. 33 Definisi Vektor
Diketahui titik $A(1,5,8)$ dan $B(6,8,1)$. Jika vektor posisi $\vec{p}$ merupakan sebuah garis berarah yang mempunyai pangkal di titik $B$ dan ujung di titik $A$ maka panjang $\vec{p}$ adalah...
$ \begin{align} & (A) \ \sqrt{83} \\ & (B) \ 64 \\ & (C) \ \sqrt{57} \\ & (D) \ 54 \\ & (E) \ \sqrt{39} \end{align} $
Diketahui titik $A(1,5,8)$ dan $B(6,8,1)$. Jika vektor posisi $\vec{p}$ merupakan sebuah garis berarah yang mempunyai pangkal di titik $B$ dan ujung di titik $A$ maka panjang $\vec{p}$ adalah...
$ \begin{align} & (A) \ \sqrt{83} \\ & (B) \ 64 \\ & (C) \ \sqrt{57} \\ & (D) \ 54 \\ & (E) \ \sqrt{39} \end{align} $
$
\begin{align}
\vec{p} &= A-B \\
&= \begin{pmatrix}
1 \\
5 \\
8
\end{pmatrix}
- \begin{pmatrix}
6 \\
8 \\
1
\end{pmatrix} \\
&= \begin{pmatrix}
-5 \\
-3 \\
7
\end{pmatrix}
\end{align}
$
Panjang $\vec{p}$ adalah :
$ \begin{align} | \vec{p} | &= \sqrt{\left( -5 \right)^{2}+\left( -3 \right)^{2}+ 7^{2}} \\ &= \sqrt{25+9+49} \\ &= \sqrt{83} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ \sqrt{83}$.
Panjang $\vec{p}$ adalah :
$ \begin{align} | \vec{p} | &= \sqrt{\left( -5 \right)^{2}+\left( -3 \right)^{2}+ 7^{2}} \\ &= \sqrt{25+9+49} \\ &= \sqrt{83} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A) \ \sqrt{83}$.
No. 34 Limit Fungsi Aljabar
$\lim\limits_{x \to 3} \dfrac{x-3}{3-\sqrt{x+6}}=\cdots$
$ \begin{align} & (A) \ -6 \\ & (B) \ -3 \\ & (C) \ 0 \\ & (D) \ 3 \\ & (E) \ 6 \end{align} $
$\lim\limits_{x \to 3} \dfrac{x-3}{3-\sqrt{x+6}}=\cdots$
$ \begin{align} & (A) \ -6 \\ & (B) \ -3 \\ & (C) \ 0 \\ & (D) \ 3 \\ & (E) \ 6 \end{align} $
$
\begin{align}
& \lim\limits_{x \to 3} \dfrac{x-3}{3-\sqrt{x+6}} \\
& = \lim\limits_{x \to 3} \dfrac{x-3}{3-\sqrt{x+6}} \cdot \dfrac{3+\sqrt{x+6}}{3+\sqrt{x+6}} \\
& = \lim\limits_{x \to 3} \dfrac{ \left( x-3 \right) \left( 3+\sqrt{x+6} \right)}{9- \left(x+6 \right)} \\
& = \lim\limits_{x \to 3} \dfrac{ \left( x-3 \right) \left( 3+\sqrt{x+6} \right)}{3-x } \\
& = \lim\limits_{x \to 3} \dfrac{- \left( 3-x \right) \left( 3+\sqrt{x+6} \right)}{3-x } \\
& = \lim\limits_{x \to 3} \dfrac{- \left( 3+\sqrt{x+6} \right)}{1 } \\
& = \dfrac{- \left( 3+\sqrt{3+6} \right)}{1 } = -6
\end{align}
$
Jadi, pilihan jawaban yang BENAR adalah $(A) \ -6$.
Jadi, pilihan jawaban yang BENAR adalah $(A) \ -6$.
No. 35 Limit Tak Hingga
$\lim\limits_{x \to \infty} \sqrt{9x^{2}-24x+16}- \left( 3x+5 \right)=\cdots$
$ \begin{align} & (A) \ -\dfrac{9}{2} \\ & (B) \ -6 \\ & (C) \ 3 \\ & (D) \ 6 \\ & (E) \ \dfrac{9}{2} \end{align} $
$\lim\limits_{x \to \infty} \sqrt{9x^{2}-24x+16}- \left( 3x+5 \right)=\cdots$
$ \begin{align} & (A) \ -\dfrac{9}{2} \\ & (B) \ -6 \\ & (C) \ 3 \\ & (D) \ 6 \\ & (E) \ \dfrac{9}{2} \end{align} $
$
\begin{align}
& \lim\limits_{x \to \infty} \sqrt{9x^{2}-24x+16}- \left( 3x+5 \right) \\
&= \lim\limits_{x \to \infty} \sqrt{9x^{2}-24x+16}- \sqrt{9x^{2}+30x+25} \\
&= \dfrac{-24-30}{2\sqrt{9}} \\
&= \dfrac{-54}{2(6)} \\
&= -\dfrac{54}{12} \\
&= -\dfrac{9}{2}
\end{align}
$
Jadi, jawaban yang TEPAT adalah $(A) \ -\dfrac{9}{2}$.
Jadi, jawaban yang TEPAT adalah $(A) \ -\dfrac{9}{2}$.
No. 36 Kombinasi dan Permutasi
Dari $8$ orang pemain bola basket akan dibentuk tim inti yang terdiri dari $5$ orang pemain sesuai kebutuhan. Banyak susunan tim berbeda yang dapat dibentuk adalah...
$ \begin{align} & (A) \ 36 \\ & (B) \ 48 \\ & (C) \ 56 \\ & (D) \ 72 \\ & (E) \ 120 \end{align} $
Dari $8$ orang pemain bola basket akan dibentuk tim inti yang terdiri dari $5$ orang pemain sesuai kebutuhan. Banyak susunan tim berbeda yang dapat dibentuk adalah...
$ \begin{align} & (A) \ 36 \\ & (B) \ 48 \\ & (C) \ 56 \\ & (D) \ 72 \\ & (E) \ 120 \end{align} $
Karena $5$ orang pemain dibentuk secara acak dari $8$ pemain yang ada maka konteks kejadiannya masuk dalam kejadian Kombinasi (tidak memperhatikan urutan alias acak).
$ \begin{align} C_{5}^{8} &= \dfrac{8!}{(8-5)!5!} \\ &= \dfrac{8!}{3!5!} \\ &= \dfrac{6 \times 7 \times 8}{1 \times 2 \times 3} \\ &= 56 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 56$.
$ \begin{align} C_{5}^{8} &= \dfrac{8!}{(8-5)!5!} \\ &= \dfrac{8!}{3!5!} \\ &= \dfrac{6 \times 7 \times 8}{1 \times 2 \times 3} \\ &= 56 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 56$.
No. 37 Statistika
Perhatikan data tabel berikut.
Nilai $mean$ dari data pada tebel distibusi frekuensi di atas adalah...
$ \begin{align} & (A) \ 34,67 \\ & (B) \ 34,57 \\ & (C) \ 33,37 \\ & (D) \ 32,76 \\ & (E) \ 31,57 \end{align} $
Perhatikan data tabel berikut.
Nilai $mean$ dari data pada tebel distibusi frekuensi di atas adalah...
$ \begin{align} & (A) \ 34,67 \\ & (B) \ 34,57 \\ & (C) \ 33,37 \\ & (D) \ 32,76 \\ & (E) \ 31,57 \end{align} $
Dengan menambahkan kolom nilai tengah kelas $(x_{i})$ kita akan dapatkan,
Dengan demikian nilai dari $mean$ dapat kita hitung,
$ \begin{align} \bar{x} &= \dfrac{(4 \times 22)+(7 \times 27)+(11 \times 32)+(10 \times 37)+(8 \times 42)}{4+7+11+10+8} \\ &= \dfrac{88+189+352+370+336}{40} \\ &= \dfrac{1335}{40} \\ &= 33,37 \end{align} $
Jadi, jawaban yang TEPAT adalah $(C) \ 33,37$.
Dengan demikian nilai dari $mean$ dapat kita hitung,
$ \begin{align} \bar{x} &= \dfrac{(4 \times 22)+(7 \times 27)+(11 \times 32)+(10 \times 37)+(8 \times 42)}{4+7+11+10+8} \\ &= \dfrac{88+189+352+370+336}{40} \\ &= \dfrac{1335}{40} \\ &= 33,37 \end{align} $
Jadi, jawaban yang TEPAT adalah $(C) \ 33,37$.
No. 38 Persamaan Kuadrat
Sebuah persamaan kuadrat $x^2-3x-7=0$ mempunyai akar-akar $x_{1}$ dan $x_{2}$ maka :
HTML Table Generator
Sebuah persamaan kuadrat $x^2-3x-7=0$ mempunyai akar-akar $x_{1}$ dan $x_{2}$ maka :
| Pernyataan | Benar | Salah |
|---|---|---|
| $x_{1}+x_{2}=3$ | ||
| $x_{1}x_{2}=7$ | ||
| $\dfrac{1}{x_{1}}+\dfrac{1}{x_{2}}=-\dfrac{3}{7}$ |
||
| Akar - akarnya $real$. |
Persamaan kuadrat $x^2-3x-7=0$, maka :
Pernyataan 1.
$ \begin{align} x_{1}+x_{2} &= -\dfrac{b}{a} \\ &=-\dfrac{(-3)}{1} \\ &=3 \ \text{(Benar)} \end{align} $
Pernyataan 2.
$ \begin{align} x_{1}x_{2} &= \dfrac{c}{a} \\ &=\dfrac{(-7)}{1} \\ &=-7 \ \text{(Salah)} \end{align} $
Pernyataan 3.
$ \begin{align} \dfrac{1}{x_{1}}+\dfrac{1}{x_{2}} &= \dfrac{x_{1}+x_{2}}{x_{1}x_{2}} \\ &=\dfrac{3}{-7} \\ &=-\dfrac{3}{7} \ \text{(Benar)} \end{align} $
Pernyataan 4.
Syarat mempunyai akar - akar $real$ adalah nilai diskriminannya $D \ge 0$
$ \begin{align} D &= \left( -3 \right)^{2}-4(1)(-7) \\ &= 9+28 \\ &= 37 \end{align} $
Memenuhi $D \ge 0$. (Benar)
Pernyataan 1.
$ \begin{align} x_{1}+x_{2} &= -\dfrac{b}{a} \\ &=-\dfrac{(-3)}{1} \\ &=3 \ \text{(Benar)} \end{align} $
Pernyataan 2.
$ \begin{align} x_{1}x_{2} &= \dfrac{c}{a} \\ &=\dfrac{(-7)}{1} \\ &=-7 \ \text{(Salah)} \end{align} $
Pernyataan 3.
$ \begin{align} \dfrac{1}{x_{1}}+\dfrac{1}{x_{2}} &= \dfrac{x_{1}+x_{2}}{x_{1}x_{2}} \\ &=\dfrac{3}{-7} \\ &=-\dfrac{3}{7} \ \text{(Benar)} \end{align} $
Pernyataan 4.
Syarat mempunyai akar - akar $real$ adalah nilai diskriminannya $D \ge 0$
$ \begin{align} D &= \left( -3 \right)^{2}-4(1)(-7) \\ &= 9+28 \\ &= 37 \end{align} $
Memenuhi $D \ge 0$. (Benar)
No. 39 Persamaan Kuadrat
Salah satu akar persamaan kuadrat $x^{2}−(3a−5)x+3=0$ adalah tiga kali akar yang lain. Perkalian dari nilai-nilai $a$ yang memenuhi persamaan tersebut adalah...
$ \begin{align} & (A) \ -2 \\ & (B) \ -1 \\ & (C) \ 0 \\ & (D) \ 1 \\ & (E) \ 2 \end{align} $
Salah satu akar persamaan kuadrat $x^{2}−(3a−5)x+3=0$ adalah tiga kali akar yang lain. Perkalian dari nilai-nilai $a$ yang memenuhi persamaan tersebut adalah...
$ \begin{align} & (A) \ -2 \\ & (B) \ -1 \\ & (C) \ 0 \\ & (D) \ 1 \\ & (E) \ 2 \end{align} $
Misalkan akar - akar dari persamaan kuadrat $x^{2}−(3a−5)x+3=0$ adalah $p$ dan $q$ maka :
$ \begin{align} pq &= \dfrac{c}{a} \\ p \cdot 3p &= \dfrac{3}{1} \\ 3p^{2} &= 3 \\ p^{2} &= 1 \to p= \pm 1 \end{align} $
$ \begin{align} p+q &= -\dfrac{b}{a} \\ p+3p &= -\dfrac{-(3a-5)}{1} \\ 4p &= 3a-5 \\ 4 \left( \pm 1 \right) &= 3a-5 \\ \pm 4 +5 &= 3a \\ \hline 3a &= 4+5 \to a = 3 \\ 3a &= -4+5 \to a = \dfrac{1}{3} \end{align} $
Perkalian nilai $a$ yang mungkin adalah $3 \times \dfrac{1}{3}=1$.
Jadi, jawaban yang TEPAT adalah $(D) \ 1$.
$ \begin{align} pq &= \dfrac{c}{a} \\ p \cdot 3p &= \dfrac{3}{1} \\ 3p^{2} &= 3 \\ p^{2} &= 1 \to p= \pm 1 \end{align} $
$ \begin{align} p+q &= -\dfrac{b}{a} \\ p+3p &= -\dfrac{-(3a-5)}{1} \\ 4p &= 3a-5 \\ 4 \left( \pm 1 \right) &= 3a-5 \\ \pm 4 +5 &= 3a \\ \hline 3a &= 4+5 \to a = 3 \\ 3a &= -4+5 \to a = \dfrac{1}{3} \end{align} $
Perkalian nilai $a$ yang mungkin adalah $3 \times \dfrac{1}{3}=1$.
Jadi, jawaban yang TEPAT adalah $(D) \ 1$.
No. 40 Trigonometri
Sebuah tangga memiliki panjang $6$ meter. Tangga tersebut disandarkan pada tembok rumah dengan membentuk sudut $60^{0}$ terhadap tanah. Ketinggian tembok yang dapat dicapai oleh ujung tangga dari permukaan tanah adalah...meter
$ \begin{align} & (A) \ 2\sqrt{2} \\ & (B) \ 3\sqrt{2} \\ & (C) \ 2\sqrt{3} \\ & (D) \ 3\sqrt{3} \\ & (E) \ 6\sqrt{3} \end{align} $
Sebuah tangga memiliki panjang $6$ meter. Tangga tersebut disandarkan pada tembok rumah dengan membentuk sudut $60^{0}$ terhadap tanah. Ketinggian tembok yang dapat dicapai oleh ujung tangga dari permukaan tanah adalah...meter
$ \begin{align} & (A) \ 2\sqrt{2} \\ & (B) \ 3\sqrt{2} \\ & (C) \ 2\sqrt{3} \\ & (D) \ 3\sqrt{3} \\ & (E) \ 6\sqrt{3} \end{align} $
Perhatikan gambar ilustrasi dari informasi yang diketahui berikut :
Dengan memakai kaidah trigonometri dasar maka,
$ \begin{align} \sin 60^{0} &= \dfrac{tembok}{tangga} \\ \dfrac{1}{2} \sqrt{3} &= \dfrac{tembok}{6} \\ tembok &= 3\sqrt{3} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 3\sqrt{3}$.
$ \begin{align} \sin 60^{0} &= \dfrac{tembok}{tangga} \\ \dfrac{1}{2} \sqrt{3} &= \dfrac{tembok}{6} \\ tembok &= 3\sqrt{3} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D) \ 3\sqrt{3}$.
Penutup
Nah sahabat kreatif, itulah pembahasan kita kali ini tentang 40 soal prediksi Matematika Wajib PSAJ Kelas 12 SMA Tahun 2024.Semoga bisa menjadi bahan belajar, bahan latihan yang baik buat kalian yang sedang mempersiapkan diri mengikuti Penilaian Sumatif Akhir Jenjang (PSAJ).
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !
“Janganlah pernah menyerah ketika kamu masih mampu berusaha lagi. Tidak ada kata berakhir sampai kamu berhenti mencoba.”
– Brian Dyson
– Brian Dyson