Segitiga Pascal : Rumus dan Kegunaan
Ini adalah materi bahas lengkap tentang bilangan segitiga pascal, bagaimana rumus pembentuknya dan apa kegunaannya dalam matematika.
Kalau mendengar kata "Pascal" memang ngga salah juga jika kalian lebih familiar dengar saat belajar dalam Fisika.
Segitiga pascal termasuk dalam pola bilangan dalam matematika.
Pola bilangan ini sangat menarik karena tesusun dari atas ke bawah membentuk sebuah segitiga dengan angka - angka yang simetris kanan dan kirinya.
Dengan angka paling atas adalah angka $1$ dan angka - angka tepinya juga $1$.
Layaknya sebuah permainan angka namun tersimpan banyak kegunaan dalam konsep - konsep aljabar matematika kedepannya.
Jika kita jumlah angka - angka perbarisnya kita akan mendapatkan pola bilangan :
Sebenarnya jika kita cermati, pola barisan bilangan di atas adalah sebuah pola bilangan barisan geometri dengan nilai suku pertama $1$ dan rasio $2$.
Sehingga dengan memakai konsep rumus suku ke-$n$ dari barisan geometri kita akan dengan mudah mendapatkan rumus suku ke-$n$ dari pola bilangan segitiga pascal.
$ \begin{align} U_n &= ar^{n-1} \\ &= 1 \times 2^{n-1} \\ &= 2^{n-1} \end{align} $
Dengan demikian pola bilangan segitiga pascal mengikuti rumus suku ke-$n$ :
Koefisien - koefisien ini sering juga disebut sebagai koefisien binomial dari ekspansi perpangkatan aljabar tersebut.
Lebih jelas lagi nilai - nilai koefisien perpangkatan untuk beberapa nilai $n$ kalian bisa lihat pada gambar di bawah ini.
Jadi misalkan kita mau mencari berapa hasil perpangkatan dari $(a+b)^4$ dalam segitiga pascal koefisiennya adalah $\color{red}{1,4,6,4,1}$ maka hasilnya adalah :
$ \begin{align} &(a+b)^4 \\ &= \color{red}{1}a^{4}b^{0}+\color{red}{4}a^{3}b^{1}+\color{red}{6}a^{2}b^{2}+\color{red}{4}a^{1}b^{3}+\color{red}{1}a^{0}b^{4} \\ &= a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4} \end{align} $
Penyelesaian :
$ \begin{align} &(2x+3y)^4 \\ &= \color{red}{1}(2x)^{4}(3y)^{0}+\color{red}{4}(2x)^{3}(3y)^{1}+\color{red}{6}(2x)^{2}(3y)^{2}+\color{red}{4}(2x)^{1}(3y)^{3}+\color{red}{1}(2x)^{0}(3y)^{4} \\ &= \color{red}{1} \left( 16x^{4} \right)+\color{red}{4} \left( 8x^{3} \right)(3y)+\color{red}{6} \left( 4x^{2} \right) \left( 9y^{2} \right)+\color{red}{4} \left( 2x \right) \left( 27y^{3} \right)+\color{red}{1}\left( 81y^{4} \right) \\ &= 16x^{4}+96x^{3}y+216x^{2}y^{2}+216xy^{3}+81y^{4} \end{align} $
Jadi, koefisien dari bentuk $x^{3}y$ pada ekspansi $(2x+3y)^{4}$ adalah $96$ ($C$).
Dia tidak mengambil pendidikan resmi, tetapi Pascal memang sudah dikenal cerdas.
Diusianya yang masih kecil 12 tahun, Blaise sudah berhasil membuat alat mesin penghitung.
Saat itu ayahnya, Etienne Pascal adalah seorang petugas penarik pajak. Mesin hitung yang diciptakan Blaise Pascal membantu pekerjaan ayahnya di bidang penarik pajak tersebut.
Kemudian, Blaise membantu ayahnya menghitung penerimaan pajak.
Blaise Pascal menemukan teori segitiga pascal ini saat usianya 16 tahun.
Dalam teori tersebut, Blaise menjelaskan titik-titik singgung pada sisi-sisi sebuah segienam kerucut di satu titik.
Teori segitiga Pascal dipakai untuk menghitung pola bilangan yang membentuk segitiga tertentu. Teorema ini menjadi teori dasar bidang geometri proyektif.
Selain teori segitiga pascal, Blaise berhasil melakukan beberapa penelitian.
Dia menemukan prinsip kerja barometer sebagai alat pengukur tekanan udara. Dia juga menemukan rancang bangunan segienam (hexagram) dan sistem kerja dari arloji.
Blaise Pascal mengembangkan mesin hitung dan berhasil membuat prototipe untuk kalkulator mekanik. Temuan mesin hitung ini diberi nama kalkulator Pascal (Pascalines) yang dikerjakan selama tiga tahun (1642-1644).
Sering - sering lah latihan agar kalian makin paham dengan apa yang sudah dipelajari.
Segitiga pascal termasuk dalam pola bilangan dalam matematika.
Pola bilangan ini sangat menarik karena tesusun dari atas ke bawah membentuk sebuah segitiga dengan angka - angka yang simetris kanan dan kirinya.
Dengan angka paling atas adalah angka $1$ dan angka - angka tepinya juga $1$.
Layaknya sebuah permainan angka namun tersimpan banyak kegunaan dalam konsep - konsep aljabar matematika kedepannya.
Rumus Pola Segitiga Pascal
Pola segitiga pascal kita peroleh dengan menjumlah angka tiap baris dari kiri ke kanan atau sebaliknya.
$1 \ , \ 2 \ , \ 4 \ , \ 8 \ , \ 16 \ , \cdots $
Sebenarnya jika kita cermati, pola barisan bilangan di atas adalah sebuah pola bilangan barisan geometri dengan nilai suku pertama $1$ dan rasio $2$.
Sehingga dengan memakai konsep rumus suku ke-$n$ dari barisan geometri kita akan dengan mudah mendapatkan rumus suku ke-$n$ dari pola bilangan segitiga pascal.
$ \begin{align} U_n &= ar^{n-1} \\ &= 1 \times 2^{n-1} \\ &= 2^{n-1} \end{align} $
Dengan demikian pola bilangan segitiga pascal mengikuti rumus suku ke-$n$ :
$U_n=2^{n-1}$
Kegunaan Segitiga Pascal
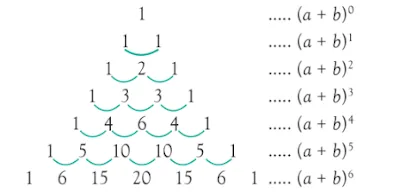
Salah satu kegunaan dari pola bilangan pada segitiga pascal adalah digunakan untuk menentukan koefisien - koefisien pada ekspansi perpangkatan aljabar $(a+b)^{n}$ untuk $n$ bilangan asli.Koefisien - koefisien ini sering juga disebut sebagai koefisien binomial dari ekspansi perpangkatan aljabar tersebut.
Lebih jelas lagi nilai - nilai koefisien perpangkatan untuk beberapa nilai $n$ kalian bisa lihat pada gambar di bawah ini.
$ \begin{align} &(a+b)^4 \\ &= \color{red}{1}a^{4}b^{0}+\color{red}{4}a^{3}b^{1}+\color{red}{6}a^{2}b^{2}+\color{red}{4}a^{1}b^{3}+\color{red}{1}a^{0}b^{4} \\ &= a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4} \end{align} $
Contoh Soal Kegunaan Segitiga Pascal
Biar makin paham kegunaan dari pola bilangan segitiga pascal kalian bisa cermati contoh soal berikut ini ya.
Nilai koefisien dari bentuk $x^{3}y$ pada ekspansi $(2x+3y)^{4}$ adalah ...
$ \begin{align} & A. \ 16 \\ & B. \ 81 \\ & C. \ 96 \\ & D. \ 128 \\ & E. \ 216 \\ \end{align} $
$ \begin{align} & A. \ 16 \\ & B. \ 81 \\ & C. \ 96 \\ & D. \ 128 \\ & E. \ 216 \\ \end{align} $
Penyelesaian :
$ \begin{align} &(2x+3y)^4 \\ &= \color{red}{1}(2x)^{4}(3y)^{0}+\color{red}{4}(2x)^{3}(3y)^{1}+\color{red}{6}(2x)^{2}(3y)^{2}+\color{red}{4}(2x)^{1}(3y)^{3}+\color{red}{1}(2x)^{0}(3y)^{4} \\ &= \color{red}{1} \left( 16x^{4} \right)+\color{red}{4} \left( 8x^{3} \right)(3y)+\color{red}{6} \left( 4x^{2} \right) \left( 9y^{2} \right)+\color{red}{4} \left( 2x \right) \left( 27y^{3} \right)+\color{red}{1}\left( 81y^{4} \right) \\ &= 16x^{4}+96x^{3}y+216x^{2}y^{2}+216xy^{3}+81y^{4} \end{align} $
Jadi, koefisien dari bentuk $x^{3}y$ pada ekspansi $(2x+3y)^{4}$ adalah $96$ ($C$).
Sejarah Segitiga Pascal
Dialah Blaise Pascal sang penemu dari pola bilangan segitiga pascal. Blaise lahir di Clermont-Ferrand, Perancis, 19 Juni 1623.
Diusianya yang masih kecil 12 tahun, Blaise sudah berhasil membuat alat mesin penghitung.
Saat itu ayahnya, Etienne Pascal adalah seorang petugas penarik pajak. Mesin hitung yang diciptakan Blaise Pascal membantu pekerjaan ayahnya di bidang penarik pajak tersebut.
Kemudian, Blaise membantu ayahnya menghitung penerimaan pajak.
Blaise Pascal menemukan teori segitiga pascal ini saat usianya 16 tahun.
Dalam teori tersebut, Blaise menjelaskan titik-titik singgung pada sisi-sisi sebuah segienam kerucut di satu titik.
Teori segitiga Pascal dipakai untuk menghitung pola bilangan yang membentuk segitiga tertentu. Teorema ini menjadi teori dasar bidang geometri proyektif.
Selain teori segitiga pascal, Blaise berhasil melakukan beberapa penelitian.
Dia menemukan prinsip kerja barometer sebagai alat pengukur tekanan udara. Dia juga menemukan rancang bangunan segienam (hexagram) dan sistem kerja dari arloji.
Blaise Pascal mengembangkan mesin hitung dan berhasil membuat prototipe untuk kalkulator mekanik. Temuan mesin hitung ini diberi nama kalkulator Pascal (Pascalines) yang dikerjakan selama tiga tahun (1642-1644).
Penutup
Nah adik - adik sahabat kreatif, semoga dengan tulisan ini kalian jadi makin paham tentang konsep dan kegunaan dari pola segitiga pascal.Sering - sering lah latihan agar kalian makin paham dengan apa yang sudah dipelajari.
Jangan lupa untuk share ke sahabat atau teman - teman jika pembahasan ini bermanfaat.
Selamat Belajar !
"Usaha akan membuahkan hasil setelah seseorang tidak menyerah." – Napoleon Hill
