Barisan Fibonacci: Misteri Angka yang Selalu Ada di Sekitar Kita
Sebuah barisan yang terkenal banget karena perannya yang membawa khasanah ilmu matematika ke level yang lebih tinggi pada $800$ tahun yang lalu.
Barisan Fibonacci itu kayak kode rahasia yang tersembunyi di mana-mana, dari alam sampai teknologi.
Yang bikin lebih keren, barisan ini ternyata simpel banget, tapi dampaknya besar banget.
Yuk, kita bahas bareng-bareng!
Apa Itu Barisan Fibonacci?
Oke, pertama-tama kita kenalan dulu sama si Fibonacci.Barisan Fibonacci itu adalah deretan angka yang dimulai dari $0$ dan $1$, terus angka berikutnya selalu didapat dengan cara menjumlahkan dua angka sebelumnya.
Jadi, bentuknya kayak gini: \[ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... \] dan seterusnya. Gampang banget, kan?
Kalau mau ngitung angka berikutnya, tinggal tambahin aja angka sebelumnya.
Misalnya, setelah $55$, angka berikutnya adalah $55 + 34 = 89$.
Terus aja kayak gitu sampai nggak ada ujungnya. Barisan ini pertama kali dikenalin sama Leonardo dari Pisa, seorang matematikawan Italia yang hidup di abad ke-13.
Nama bekennya adalah Fibonacci, dan dia yang pertama kali ngeh soal barisan angka ini.
Sejarah Ditemukannya Barisan Fibonacci
Leonardo da Pisa atau Fibonacci pertama memperkenalkan barisan ini dalam bukunya yang berjudul "Liber Abaci" (Kitab Perhitungan), yang diterbitkan pada tahun 1202.
Dalam buku itu, Fibonacci menggunakan barisan ini untuk menjelaskan soal reproduksi kelinci.
Kisah Penemuan Barisan Fibonacci:
Soalnya berbunyi kira-kira seperti ini:- Misalkan ada sepasang kelinci jantan dan betina yang baru lahir.
- Dalam sebulan, mereka tumbuh dewasa dan bisa menghasilkan pasangan kelinci baru.
- Pasangan kelinci baru juga akan mulai berkembang biak setelah sebulan.
- Berapa banyak pasangan kelinci yang ada setelah n bulan, dengan asumsi bahwa tidak ada kelinci yang mati?
Kenapa Barisan Fibonacci Itu Penting?
Nah, ini bagian serunya. Barisan Fibonacci bukan cuma angka-angka random.Angka ini punya hubungan erat dengan banyak hal di dunia nyata.
Bahkan, bisa dibilang barisan ini kayak DNA-nya alam semesta.
Contohnya? Nih:
- Daun Tumbuhan
Coba deh perhatikan bunga matahari. Jumlah kelopaknya biasanya ada di salah satu angka Fibonacci, misalnya $34$ atau $55$. Bahkan cara daun tumbuh di batang tanaman juga sering mengikuti pola ini. - Cangkang Keong
Kamu pernah lihat cangkang keong yang bentuknya spiral? Itu juga nggak asal bentuk. Spiralnya ternyata sesuai dengan rasio Fibonacci. Makanya, bentuknya kelihatan alami banget. - Tubuh Manusia
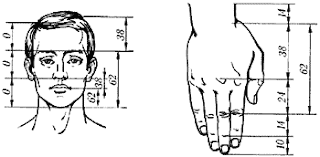
Tubuh kita sendiri ternyata penuh sama angka Fibonacci. Contohnya, jumlah ruas jari tangan, tulang-tulang di tubuh, bahkan proporsi wajah kita. Keren banget, kan? - Galaxy dan Alam Semesta
Spiral di galaksi juga ternyata punya hubungan sama barisan Fibonacci. Jadi, angka ini benar-benar universal.
Barisan ini ternyata punya hubungan erat dengan fenomena alam, geometri, dan rasio emas (golden ratio).
Oleh karena itu, meskipun barisan ini ditemukan hampir $800$ tahun lalu, dampaknya masih terasa hingga sekarang di berbagai bidang, termasuk seni, sains, dan teknologi.
Jadi, bisa dibilang Fibonacci bukan hanya matematikawan biasa, tetapi salah satu pelopor besar yang membawa matematika ke level yang lebih tinggi di zamannya! 🚀
Golden Ratio: Teman Setia Fibonacci
Ngomongin Fibonacci nggak lengkap kalau nggak bahas golden ratio.Jadi gini, kalau kamu bagi dua angka Fibonacci yang berurutan, hasilnya bakal mendekati $1,618$.
Golden ratio ini sering dianggap sebagai ukuran "keindahan".
Misalnya, desain bangunan kuno kayak Parthenon di Yunani, lukisan Mona Lisa, sampai logo-logo modern kayak Apple atau Twitter.
Fibonacci di Dunia Modern
Jangan kira Fibonacci cuma ada di alam atau seni.Di dunia modern, barisan ini juga dipake di banyak bidang, lho.
Contohnya:
- Teknologi Komputer
Dalam coding dan algoritma, Fibonacci sering dipake buat ngatur struktur data atau sistem yang butuh efisiensi. - Pasar Saham
Trader di pasar saham sering pake pola Fibonacci buat ngebantu mereka menganalisis harga. Mereka percaya angka ini bisa bantu mereka bikin keputusan investasi. - Desain Digital Buat para desainer grafis, Fibonacci sering dipake buat bikin layout yang enak dilihat. Makanya, hasilnya selalu kelihatan rapi dan estetis.
Serunya Belajar Fibonacci
Belajar barisan Fibonacci itu nggak cuma buat sekadar tau angka-angkanya, tapi juga biar kita makin sadar betapa matematika itu sebenarnya ada di sekitar kita.Dari pola-pola kecil di daun sampai desain teknologi canggih, semuanya bisa dikaitin sama barisan ini.
Coba deh, lain kali kalau kamu lihat hal-hal di sekitar, pikirin: "Eh, ada Fibonacci-nya nggak ya?"
Siapa tau kamu nemuin pola Fibonacci di hal-hal yang nggak pernah kamu sangka sebelumnya.
Penutup
Barisan Fibonacci itu kayak kode rahasia yang bikin kita makin sadar kalau alam semesta itu luar biasa teratur dan indah.Bahkan, meskipun kelihatannya cuma deretan angka, dampaknya ternyata bisa kita lihat di mana-mana.
Jadi, kapan lagi belajar matematika bisa sekeren ini?
Sekarang, giliran kamu buat nyari pola Fibonacci di sekitarmu.
Siapa tau kamu nemuin sesuatu yang baru dan nggak kalah menarik.
Selamat eksplorasi, Sobat Fibonacci! 😊
"Angka adalah kunci untuk memahami dunia, dan pengetahuan tentang mereka membuka pintu ke segala ilmu." – Leonardo da Pisa
