Bikin Jago TPS! 30+ Kumpulan Soal Perbandingan dan Pembahasan Lengkap
Siapa nih yang lagi semangat belajar buat UTBK?
Kalau kamu merasa TPS (Tes Potensi Skolastik) itu kayak tantangan besar, santai aja, karena artikel ini bakal bantu kamu khususnya di bagian perbandingan.
Yuk, kita kupas tuntas cara menjinakkan soal-soal ini langsung praktek kumpulan soal dan pembahasannya, biar hasil skor TPS-mu makin meroket!
Kumpulan Soal Perbandingan dan Pembahasan
Sebelum lanjut kita disclaimer dulu nih.Kumpulan soal dibawah merupakan rangkuman dari soal - soal yang berhasil kami kumpulkan dari berbagai sumber.
Terdiri dari materi perbandingan senilai, perbandingan berbalik nilai atau bahkan perbandingan campuran (bertingkat).
Santai saja mahaminnya, nggak usah di skip - skip ya, biar makin ngerti kamunya.
Soal No.1
Untuk menyelesaikan $0,4$ bagian order percetakan dibutuhkan waktu $8$ jam. Waktu yang dibutuhkan untuk menyelesaikan sisa order percetakan tersebut adalah ... jam
$ \begin{align} & (A). 4 \\ & (B). 8 \\ & (C). 12 \\ & (D). 20 \\ & (E). 24 \end{align} $
Untuk menyelesaikan $0,4$ bagian order percetakan dibutuhkan waktu $8$ jam. Waktu yang dibutuhkan untuk menyelesaikan sisa order percetakan tersebut adalah ... jam
$ \begin{align} & (A). 4 \\ & (B). 8 \\ & (C). 12 \\ & (D). 20 \\ & (E). 24 \end{align} $
Sisa order percetakan
$=1-0,4=0,6$ bagian.
$0,4$ bagian $\to$ $8$ jam
$0,6$ bagian $\to$ $x$ jam
Sehingga,
$ \begin{align} \dfrac{0,4}{0,6} &= \dfrac{8}{x} \\ \dfrac{2}{3} &= \dfrac{8}{x} \\ 2x &= 24 \\ x &= 12 \end{align} $
Jadi, jawaban yang BENAR adalah $ (C). 12$.
$=1-0,4=0,6$ bagian.
$0,4$ bagian $\to$ $8$ jam
$0,6$ bagian $\to$ $x$ jam
Sehingga,
$ \begin{align} \dfrac{0,4}{0,6} &= \dfrac{8}{x} \\ \dfrac{2}{3} &= \dfrac{8}{x} \\ 2x &= 24 \\ x &= 12 \end{align} $
Jadi, jawaban yang BENAR adalah $ (C). 12$.
Soal No.2
Pak Hendra digaji $Rp. \ 360.000,00$ selama $3$ jam untuk memberikan pelatihan di tempat kursus. Waktu yang Pak Hendra gunakan untuk pelatihan jika beliau mendapatkan gaji $Rp. \ 7.200.000,00$ adalah ... jam
$ \begin{align} & (A). 12 \\ & (B). 20 \\ & (C). 60 \\ & (D). 140 \\ & (E). 160 \end{align} $
Pak Hendra digaji $Rp. \ 360.000,00$ selama $3$ jam untuk memberikan pelatihan di tempat kursus. Waktu yang Pak Hendra gunakan untuk pelatihan jika beliau mendapatkan gaji $Rp. \ 7.200.000,00$ adalah ... jam
$ \begin{align} & (A). 12 \\ & (B). 20 \\ & (C). 60 \\ & (D). 140 \\ & (E). 160 \end{align} $
$Rp. \ 360.000,00$ $\to$ $3$ jam
$Rp. \ 7.200.000,00$ $\to$ $x$ jam
Sehingga,
$ \begin{align} \dfrac{Rp. \ 360.000,00}{Rp. \ 7.200.000,00} &= \dfrac{3}{x} \\ \dfrac{1}{20} &= \dfrac{3}{x} \\ x &= 60 \end{align} $
Jadi, jawaban yang BENAR adalah $ (C). 60$.
$Rp. \ 7.200.000,00$ $\to$ $x$ jam
Sehingga,
$ \begin{align} \dfrac{Rp. \ 360.000,00}{Rp. \ 7.200.000,00} &= \dfrac{3}{x} \\ \dfrac{1}{20} &= \dfrac{3}{x} \\ x &= 60 \end{align} $
Jadi, jawaban yang BENAR adalah $ (C). 60$.
Soal No.3 TPS UTBK 2019
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan. Untuk membuat $300$ biskuit dengan ukuran dua kali biskuit kecil diperlukan adonan sebanyak ... kg
$ \begin{align} &(A)\ \dfrac{2}{5}x \\ &(B)\ \dfrac{5}{2}x \\ &(C)\ 2x \\ &(D)\ 5x \\ &(E)\ 10x \end{align} $
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan. Untuk membuat $300$ biskuit dengan ukuran dua kali biskuit kecil diperlukan adonan sebanyak ... kg
$ \begin{align} &(A)\ \dfrac{2}{5}x \\ &(B)\ \dfrac{5}{2}x \\ &(C)\ 2x \\ &(D)\ 5x \\ &(E)\ 10x \end{align} $
Pembuatan $120$ biskuit ukuran kecil memerlukan $x$ kg adonan, artinya untuk membuat $1$ biskuit kecil dibutuhkan $\dfrac{x}{120}$ kg adonan.
Sehingga untuk membuat $300$ biskuit yang berukuran dua kali lebih besar,
$ \begin{align} &= 300 \times 2 \times \dfrac{x}{120} \\ &= \dfrac{600}{120}x \\ &= 5x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D)\ 5x $.
Sehingga untuk membuat $300$ biskuit yang berukuran dua kali lebih besar,
$ \begin{align} &= 300 \times 2 \times \dfrac{x}{120} \\ &= \dfrac{600}{120}x \\ &= 5x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D)\ 5x $.
Soal No.4
$3$ ekor sapi dapat menghabiskan rumput pada sebidang lahan dalam $20$ hari, sedangkan $5$ ekor kambing membutuhkan waktu $40$ hari. Berapa hari rumput tersebut akan habis jika dimakan oleh $2$ ekor sapi dan $2$ ekor kambing?
$ \begin{align} & (A) \ 10 \ \text{hari} \\ & (B) \ 17 \ \text{hari} \\ & (C) \ 23 \ \text{hari} \\ & (D) \ 25 \ \text{hari} \\ & (E) \ 30 \ \text{hari} \end{align} $
$3$ ekor sapi dapat menghabiskan rumput pada sebidang lahan dalam $20$ hari, sedangkan $5$ ekor kambing membutuhkan waktu $40$ hari. Berapa hari rumput tersebut akan habis jika dimakan oleh $2$ ekor sapi dan $2$ ekor kambing?
$ \begin{align} & (A) \ 10 \ \text{hari} \\ & (B) \ 17 \ \text{hari} \\ & (C) \ 23 \ \text{hari} \\ & (D) \ 25 \ \text{hari} \\ & (E) \ 30 \ \text{hari} \end{align} $
Misalkan Sapi = $A$ dan Kambing = $B$ maka,
$\clubsuit$
$\dfrac{3}{A} = \dfrac{1}{20} \to A = 60$
$\clubsuit$$\clubsuit$
$\dfrac{5}{B} = \dfrac{1}{40} \to B = 200$
Sehingga jika sapi dan kambing bekerja sama maka,
$ \begin{align} 2A+2B &= \dfrac{1}{\frac{2}{60}+\frac{2}{200}} \\ &= \dfrac{1}{\frac{20}{600}+\frac{6}{600}} \\ &= \dfrac{600}{26} \\ &= 23 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 23 $ hari.
$\clubsuit$
$\dfrac{3}{A} = \dfrac{1}{20} \to A = 60$
$\clubsuit$$\clubsuit$
$\dfrac{5}{B} = \dfrac{1}{40} \to B = 200$
Sehingga jika sapi dan kambing bekerja sama maka,
$ \begin{align} 2A+2B &= \dfrac{1}{\frac{2}{60}+\frac{2}{200}} \\ &= \dfrac{1}{\frac{20}{600}+\frac{6}{600}} \\ &= \dfrac{600}{26} \\ &= 23 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C) \ 23 $ hari.
Soal No.5
Sebuah mobil miniatur mainan brand terkenal berencana membuat model miniatur mobil balap $F1$ dengan skala $1:20$. Jika panjang mobil tersebut pada miniatur adalah $25$ cm maka panjang sebenarnya mobil $F1$ adalah ... meter
$ \begin{align} &(A). \ 3 \\ &(B). \ 3,57 \\ &(C). \ 4,2 \\ &(D). \ 4,8 \\ &(E). \ 5 \\ \end{align} $
Sebuah mobil miniatur mainan brand terkenal berencana membuat model miniatur mobil balap $F1$ dengan skala $1:20$. Jika panjang mobil tersebut pada miniatur adalah $25$ cm maka panjang sebenarnya mobil $F1$ adalah ... meter
$ \begin{align} &(A). \ 3 \\ &(B). \ 3,57 \\ &(C). \ 4,2 \\ &(D). \ 4,8 \\ &(E). \ 5 \\ \end{align} $
Kita hitung,
$ \begin{align} \dfrac{P_{miniatur}}{P_{mobil}} &= \dfrac{1}{20} \\ \\ \dfrac{25}{P_{mobil}} &= \dfrac{1}{20} \\ \\ P_{mobil} &= 25 \times 20 \\ &= 500 \end{align} $
Jadi, panjang mobil F1 sebenarnya adalah $500$ cm atau $5$ meter.
Jawaban yang BENAR adalah sesuai dengan pilihan $(E). \ 5$
$ \begin{align} \dfrac{P_{miniatur}}{P_{mobil}} &= \dfrac{1}{20} \\ \\ \dfrac{25}{P_{mobil}} &= \dfrac{1}{20} \\ \\ P_{mobil} &= 25 \times 20 \\ &= 500 \end{align} $
Jadi, panjang mobil F1 sebenarnya adalah $500$ cm atau $5$ meter.
Jawaban yang BENAR adalah sesuai dengan pilihan $(E). \ 5$
Soal No.6
Terdapat $42$ siswa mengikuti kelas paduan suara. $31$ siswa yang mengikuti kelas paduan suara adalah perempuan. Di antara proporsi berikut yang digunakan untuk menentukan $x$, yakni prosentase siswa laki - laki yang mengikuti kelas paduan suara adalah ...
$ \begin{align} &(A). \ \dfrac{31}{42}=\dfrac{x}{100} \\ \\ &(B). \ \dfrac{11}{31}=\dfrac{x}{100} \\ \\ &(C). \ \dfrac{31}{11}=\dfrac{x}{100} \\ \\ &(D). \ \dfrac{11}{42}=\dfrac{x}{100} \\ \\ &(E). \ \dfrac{42}{11}=\dfrac{x}{100} \end{align} $
Terdapat $42$ siswa mengikuti kelas paduan suara. $31$ siswa yang mengikuti kelas paduan suara adalah perempuan. Di antara proporsi berikut yang digunakan untuk menentukan $x$, yakni prosentase siswa laki - laki yang mengikuti kelas paduan suara adalah ...
$ \begin{align} &(A). \ \dfrac{31}{42}=\dfrac{x}{100} \\ \\ &(B). \ \dfrac{11}{31}=\dfrac{x}{100} \\ \\ &(C). \ \dfrac{31}{11}=\dfrac{x}{100} \\ \\ &(D). \ \dfrac{11}{42}=\dfrac{x}{100} \\ \\ &(E). \ \dfrac{42}{11}=\dfrac{x}{100} \end{align} $
Jumlah siswa laki - laki $=42-31=11$ siswa.
Sehingga perbandingan untuk menentukan prosentase siswa laki - laki adalah :
$ \dfrac{11}{42}=\dfrac{x}{100} $
Jadi, pilihan jawaban yang BENAR adalah $(D.)$
Sehingga perbandingan untuk menentukan prosentase siswa laki - laki adalah :
$ \dfrac{11}{42}=\dfrac{x}{100} $
Jadi, pilihan jawaban yang BENAR adalah $(D.)$
Soal No.7
Perbandingan umur kakak dan ibu saat ini adalah $1 : 2$ , sedangkan perbandingan ibu dan ayah adalah $8 : 11$. Maka perbandingan umur kakak dan ayah yang benar adalah ...
$ \begin{align} &(A). \ 1 : 11 \\ &(B). \ 2 : 11 \\ &(C). \ 2 : 8 \\ &(D). \ 4 : 11 \\ &(E). \ 4 : 22 \end{align} $
Perbandingan umur kakak dan ibu saat ini adalah $1 : 2$ , sedangkan perbandingan ibu dan ayah adalah $8 : 11$. Maka perbandingan umur kakak dan ayah yang benar adalah ...
$ \begin{align} &(A). \ 1 : 11 \\ &(B). \ 2 : 11 \\ &(C). \ 2 : 8 \\ &(D). \ 4 : 11 \\ &(E). \ 4 : 22 \end{align} $
Cara mengerjakan soal ini kita bisa pakai sistem tabel seperti di bawah.
Cukup samakan pembanding umur ibu pada nilai kedua perbandingannya.
Perbandingan umur kakak dan ayah $\to 4 : 11$.
Jadi, pilihan jawaban yang BENAR adalah $(D.) \ 4 : 11$
Cukup samakan pembanding umur ibu pada nilai kedua perbandingannya.
Jadi, pilihan jawaban yang BENAR adalah $(D.) \ 4 : 11$
Soal No.8
Jika $2p \lt k$ dan $10q \gt 8k$ maka pernyataan berikut yang BENAR adalah …
$ \begin{align} &(A). \ \dfrac{p}{q} \lt \dfrac{5}{8} \\ &(B). \ \dfrac{p}{q} \lt \dfrac{2}{8} \\ &(C). \ \dfrac{p}{k} \lt \dfrac{5}{2} \\ &(D). \ \dfrac{k}{q} \lt \dfrac{-5}{8} \\ &(E). \ \dfrac{q}{p} \lt \dfrac{5}{8} \end{align} $
Jika $2p \lt k$ dan $10q \gt 8k$ maka pernyataan berikut yang BENAR adalah …
$ \begin{align} &(A). \ \dfrac{p}{q} \lt \dfrac{5}{8} \\ &(B). \ \dfrac{p}{q} \lt \dfrac{2}{8} \\ &(C). \ \dfrac{p}{k} \lt \dfrac{5}{2} \\ &(D). \ \dfrac{k}{q} \lt \dfrac{-5}{8} \\ &(E). \ \dfrac{q}{p} \lt \dfrac{5}{8} \end{align} $
\[ 2p \lt k \to 16p \lt 8k \]
Dengan sifat transitif pertidaksamaan kita bisa gabung kedua persamaannya menjadi :
\[ 16p \lt 8k \lt 10q \]
Sehingga,
$ \begin{align} 16p &\lt 10q \\ \\ \dfrac{16p}{q} &\lt 10 \\ \dfrac{p}{q} &\lt \dfrac{10}{16} \to \dfrac{p}{q} \lt \dfrac{5}{8} \\ \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A). \ \dfrac{p}{q} \lt \dfrac{5}{8}$
$ \begin{align} 16p &\lt 10q \\ \\ \dfrac{16p}{q} &\lt 10 \\ \dfrac{p}{q} &\lt \dfrac{10}{16} \to \dfrac{p}{q} \lt \dfrac{5}{8} \\ \end{align} $
Jadi, pilihan jawaban yang BENAR adalah $(A). \ \dfrac{p}{q} \lt \dfrac{5}{8}$
Soal No.9
Suatu persediaan pakan dalam sebuah peternakan cukup untuk $30$ hari diberikan kepada $100$ ekor ayam. Jika karena suatu hal ternyata $40$ ekor ayam mati, maka persediaan pakan akan cukup untuk ... hari
$ \begin{align} &(A). \ 10 \\ &(B). \ 20 \\ &(C). \ 30 \\ &(D). \ 40 \\ &(E). \ 50 \end{align} $
Suatu persediaan pakan dalam sebuah peternakan cukup untuk $30$ hari diberikan kepada $100$ ekor ayam. Jika karena suatu hal ternyata $40$ ekor ayam mati, maka persediaan pakan akan cukup untuk ... hari
$ \begin{align} &(A). \ 10 \\ &(B). \ 20 \\ &(C). \ 30 \\ &(D). \ 40 \\ &(E). \ 50 \end{align} $
$40$ ekor ayam mati sisa ayam tinggal $60$ ekor.
$100$ ekor $\to$ $30$ hari
$60$ ekor $\to$ $x$ hari
Karena ayamnya makin sedikit, jadi persedian pakannya akan semakin lama harusnya.
Jadi, masuk dalam kategori perbandingan berbalik nilai.
Sehingga,
$ \begin{align} \dfrac{100}{60} &= \dfrac{x}{30} \\ 60x &= 3000 \\ x &= 50 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 50$.
$100$ ekor $\to$ $30$ hari
$60$ ekor $\to$ $x$ hari
Karena ayamnya makin sedikit, jadi persedian pakannya akan semakin lama harusnya.
Jadi, masuk dalam kategori perbandingan berbalik nilai.
Sehingga,
$ \begin{align} \dfrac{100}{60} &= \dfrac{x}{30} \\ 60x &= 3000 \\ x &= 50 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 50$.
Soal No.10
Perbandingan tinggi badan Amir dan Doni adalah $7:8$. Jika badan Amir adalah $133$ cm, maka tinggi badan Doni adalah ...
$ \begin{align} &(A). \ 148 \\ &(B). \ 150 \\ &(C). \ 152 \\ &(D). \ 154 \\ &(E). \ 156 \end{align} $
Perbandingan tinggi badan Amir dan Doni adalah $7:8$. Jika badan Amir adalah $133$ cm, maka tinggi badan Doni adalah ...
$ \begin{align} &(A). \ 148 \\ &(B). \ 150 \\ &(C). \ 152 \\ &(D). \ 154 \\ &(E). \ 156 \end{align} $
Misal tinggi badan Doni adalah $x$ cm.
$ \begin{align} \dfrac{7}{8} &= \dfrac{133}{x} \\ 7x &= 1064 \\ x &= 152 \end{align} $
Jadi, jawaban yang BENAR adalah $(C). \ 152$.
$ \begin{align} \dfrac{7}{8} &= \dfrac{133}{x} \\ 7x &= 1064 \\ x &= 152 \end{align} $
Jadi, jawaban yang BENAR adalah $(C). \ 152$.
Soal No.11
Lima belas mangkok diisi dengan $90$ telor matang. Dapat diperkirakan bahwa telor matang yang ada dalam $7$ mangkok adalah ...
$ \begin{align} &(A). \ 21 \\ &(B). \ 28 \\ &(C). \ 35 \\ &(D). \ 42 \\ &(E). \ 45 \end{align} $
Lima belas mangkok diisi dengan $90$ telor matang. Dapat diperkirakan bahwa telor matang yang ada dalam $7$ mangkok adalah ...
$ \begin{align} &(A). \ 21 \\ &(B). \ 28 \\ &(C). \ 35 \\ &(D). \ 42 \\ &(E). \ 45 \end{align} $
$
\begin{align}
\dfrac{15}{7} &= \dfrac{90}{x} \\
15x &= 630 \\
x &= 42
\end{align}
$
Jadi, jawaban yang BENAR adalah $(D). \ 42$.
Jadi, jawaban yang BENAR adalah $(D). \ 42$.
Soal No.12
Doni mempunyai kelereng sebanyak dua kali kelereng Surya. Jika Doni memberikan $20$ kelereng kepada Surya, jumlah kelereng Surya menjadi tiga kali jumlah kelereng Doni. Jumlah kelereng Doni mula - mula adalah ...
$ \begin{align} &(A). \ 24 \\ &(B). \ 27 \\ &(C). \ 28 \\ &(D). \ 30 \\ &(E). \ 32 \end{align} $
Doni mempunyai kelereng sebanyak dua kali kelereng Surya. Jika Doni memberikan $20$ kelereng kepada Surya, jumlah kelereng Surya menjadi tiga kali jumlah kelereng Doni. Jumlah kelereng Doni mula - mula adalah ...
$ \begin{align} &(A). \ 24 \\ &(B). \ 27 \\ &(C). \ 28 \\ &(D). \ 30 \\ &(E). \ 32 \end{align} $
Misal :
$D \to$ banyak kelereng Doni.
$S \to$ banyak kelereng Surya.
Diketahui :
$D = 2 S$
$3(D-20) = S+20$
Sehingga,
$ \begin{align} 3(D-20) &= S+20 \\ 3D - 60 &= S +20 \\ \\ \text{substitusi} \ D = 2 S \\ \\ 3(2S) - 60 &= S +20 \\ 5S &= 80 \\ S &= 16 \\ \\ D &= 2S \\ &= 2(16) = 32 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 32$.
$D \to$ banyak kelereng Doni.
$S \to$ banyak kelereng Surya.
Diketahui :
$D = 2 S$
$3(D-20) = S+20$
Sehingga,
$ \begin{align} 3(D-20) &= S+20 \\ 3D - 60 &= S +20 \\ \\ \text{substitusi} \ D = 2 S \\ \\ 3(2S) - 60 &= S +20 \\ 5S &= 80 \\ S &= 16 \\ \\ D &= 2S \\ &= 2(16) = 32 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 32$.
Soal No.13
Seorang peternak ayam memiliki persediaan makanan untuk $150$ ekor ayam selama $6$ hari. Jika ia membeli lagi $30$ ekor ayam lagi, persediaan makanan yang ada akan habis dalam ... hari
$ \begin{align} &(A). \ 3 \\ &(B). \ 4 \\ &(C). \ 5 \\ &(D). \ 6 \\ &(E). \ 8 \end{align} $
Seorang peternak ayam memiliki persediaan makanan untuk $150$ ekor ayam selama $6$ hari. Jika ia membeli lagi $30$ ekor ayam lagi, persediaan makanan yang ada akan habis dalam ... hari
$ \begin{align} &(A). \ 3 \\ &(B). \ 4 \\ &(C). \ 5 \\ &(D). \ 6 \\ &(E). \ 8 \end{align} $
Perbandingan berbalik nilai.
$150$ ekor $ \to 6$ hari
$150+30$ ekor $\to x$ hari
$ \begin{align} \dfrac{150}{180} &= \dfrac{x}{6} \\ \dfrac{5}{6} &= \dfrac{x}{6} \\ x &= 5 \end{align} $
Jadi, jawaban yang BENAR adalah $(C). \ 5$.
$150$ ekor $ \to 6$ hari
$150+30$ ekor $\to x$ hari
$ \begin{align} \dfrac{150}{180} &= \dfrac{x}{6} \\ \dfrac{5}{6} &= \dfrac{x}{6} \\ x &= 5 \end{align} $
Jadi, jawaban yang BENAR adalah $(C). \ 5$.
Soal No.14
Perbandingan antara $3$ km dengan $150$ m adalah ...
$ \begin{align} &(A). \ 1 : 5 \\ &(B). \ 1 : 50 \\ &(C). \ 3 : 5 \\ &(D). \ 20 : 1 \\ &(E). \ 30 : 1 \end{align} $
Perbandingan antara $3$ km dengan $150$ m adalah ...
$ \begin{align} &(A). \ 1 : 5 \\ &(B). \ 1 : 50 \\ &(C). \ 3 : 5 \\ &(D). \ 20 : 1 \\ &(E). \ 30 : 1 \end{align} $
$3$ km $= 3.000$ m
$ \dfrac{3.000}{150} = \dfrac{20}{1} $
Jadi, jawaban yang BENAR adalah $(D). \ 20 : 1$.
$ \dfrac{3.000}{150} = \dfrac{20}{1} $
Jadi, jawaban yang BENAR adalah $(D). \ 20 : 1$.
Soal No.15
Jumlah uang Andi dan Yoga adalah $Rp. \ 96.000,00$. Jika perbandingan uang mereka $9:7$ maka selisih uang mereka adalah ...
$ \begin{align} &(A). \ Rp. \ 10.000,00 \\ &(B). \ Rp. \ 12.000,00 \\ &(C). \ Rp. \ 15.000,00 \\ &(D). \ Rp. \ 18.000,00 \\ &(E). \ Rp. \ 24.000,00 \end{align} $
Jumlah uang Andi dan Yoga adalah $Rp. \ 96.000,00$. Jika perbandingan uang mereka $9:7$ maka selisih uang mereka adalah ...
$ \begin{align} &(A). \ Rp. \ 10.000,00 \\ &(B). \ Rp. \ 12.000,00 \\ &(C). \ Rp. \ 15.000,00 \\ &(D). \ Rp. \ 18.000,00 \\ &(E). \ Rp. \ 24.000,00 \end{align} $
$
\begin{align}
\dfrac{\text{Jumlah}}{\text{Selisih}} &= \dfrac{9+7}{9-7} \\ \\
\dfrac{96.000}{\text{Selisih}} &= \dfrac{16}{2} \\ \\
\text{Selisih} &= \dfrac{2 \times 96.000}{16} \\
&= 12.000
\end{align}
$
Jadi, jawaban yang BENAR adalah $(B). \ Rp. \ 12.000,00$.
Jadi, jawaban yang BENAR adalah $(B). \ Rp. \ 12.000,00$.
Soal No.16
Sebuah mesin di suatu pabrik minuman mampu memasang tutup botol untuk $14$ botol dalam waktu $84$ detik. Banyak botol yang dapat ditutup oleh mesin dalam waktu $2$ menit adalah ... botol
$ \begin{align} &(A). \ 16 \\ &(B). \ 20 \\ &(C). \ 25 \\ &(D). \ 28 \\ &(E). \ 35 \end{align} $
Sebuah mesin di suatu pabrik minuman mampu memasang tutup botol untuk $14$ botol dalam waktu $84$ detik. Banyak botol yang dapat ditutup oleh mesin dalam waktu $2$ menit adalah ... botol
$ \begin{align} &(A). \ 16 \\ &(B). \ 20 \\ &(C). \ 25 \\ &(D). \ 28 \\ &(E). \ 35 \end{align} $
$2$ menit $= 120$ detik.
$14$ botol $ \to 84$ detik
$x$ ekor $\to 120$ detik
$ \begin{align} \dfrac{14}{x} &= \dfrac{84}{120} \\ \\ \dfrac{14}{x} &= \dfrac{7}{10} \\ \\ 7x &= 140 \\ x &= 20 \end{align} $
Jadi, jawaban yang BENAR adalah $(B). \ 20$.
$14$ botol $ \to 84$ detik
$x$ ekor $\to 120$ detik
$ \begin{align} \dfrac{14}{x} &= \dfrac{84}{120} \\ \\ \dfrac{14}{x} &= \dfrac{7}{10} \\ \\ 7x &= 140 \\ x &= 20 \end{align} $
Jadi, jawaban yang BENAR adalah $(B). \ 20$.
Soal No.17
Tari bersepeda mengelilingi kompleks dengan kecepatan tetap yaitu $5$ km/jam. Setelah $30$ menit, ia menempuh jarak $2,5$ km. Waktu yang diperlukan Tari agar menempuh jarak sejauh $4$ km adalah ... menit
$ \begin{align} &(A). \ 45 \\ &(B). \ 46 \\ &(C). \ 47 \\ &(D). \ 48 \\ &(E). \ 49 \end{align} $
Tari bersepeda mengelilingi kompleks dengan kecepatan tetap yaitu $5$ km/jam. Setelah $30$ menit, ia menempuh jarak $2,5$ km. Waktu yang diperlukan Tari agar menempuh jarak sejauh $4$ km adalah ... menit
$ \begin{align} &(A). \ 45 \\ &(B). \ 46 \\ &(C). \ 47 \\ &(D). \ 48 \\ &(E). \ 49 \end{align} $
Karena kecepatannya tetap maka bisa kita hiraukan.
$30$ menit $ \to 2,5$ km
$a$ menit $\to 4$ km
$ \begin{align} \dfrac{30}{a} &= \dfrac{2,5}{4} \\ \\ 2,5a &= 4 \times 30 \\ a &= 48 \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 48$.
$30$ menit $ \to 2,5$ km
$a$ menit $\to 4$ km
$ \begin{align} \dfrac{30}{a} &= \dfrac{2,5}{4} \\ \\ 2,5a &= 4 \times 30 \\ a &= 48 \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 48$.
Soal No.18
HTML Table Generator
Tabel di atas menunjukkan waktu yang dibutuhkan oleh seorang perajin untuk membuat sepatu. Lama waktu yang diperlukan untuk membuat $75$ pasang sepatu adalah ... hari
$ \begin{align} &(A). \ 42 \\ &(B). \ 40 \\ &(C). \ 39 \\ &(D). \ 36 \\ &(E). \ 30 \end{align} $
| Banyak sepatu (pasang) | $60$ | $75$ |
| Waktu Pengerjaan (hari) | $24$ | $x$ |
$ \begin{align} &(A). \ 42 \\ &(B). \ 40 \\ &(C). \ 39 \\ &(D). \ 36 \\ &(E). \ 30 \end{align} $
$60$ pasang $ \to 24$ hari
$75$ pasang $\to y$ hari
$ \begin{align} \dfrac{60}{75} &= \dfrac{24}{y} \\ \\ y &= \dfrac{75 \times 24}{60} \\ y &= 30 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 30$.
$75$ pasang $\to y$ hari
$ \begin{align} \dfrac{60}{75} &= \dfrac{24}{y} \\ \\ y &= \dfrac{75 \times 24}{60} \\ y &= 30 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 30$.
Soal No.19
Ukuran sebuah foto adalah $6$ cm $\times$ $9$ cm. Foto tersebut dipebesar sehingga sisi panjang menjadi $72$ cm. Perbandingan luas foto sebelum dan sesudah diperbesar adalah ...
$ \begin{align} &(A). \ 1 : 64 \\ &(B). \ 1 : 32 \\ &(C). \ 1 : 16 \\ &(D). \ 1 : 8 \\ &(E). \ 1 : 6 \end{align} $
Ukuran sebuah foto adalah $6$ cm $\times$ $9$ cm. Foto tersebut dipebesar sehingga sisi panjang menjadi $72$ cm. Perbandingan luas foto sebelum dan sesudah diperbesar adalah ...
$ \begin{align} &(A). \ 1 : 64 \\ &(B). \ 1 : 32 \\ &(C). \ 1 : 16 \\ &(D). \ 1 : 8 \\ &(E). \ 1 : 6 \end{align} $
$
\begin{align}
\dfrac{6}{9} = \dfrac{l}{24} \to \ & l=48 \ \text{cm} \\ \\
\dfrac{\text{Luas Lama}}{\text{Luas Baru}} &= \dfrac{6 \times 9}{48 \times 72} = \dfrac{1}{64} \\
\end{align}
$
Jadi, jawaban yang BENAR adalah $(A). \ 1 : 64$.
Jadi, jawaban yang BENAR adalah $(A). \ 1 : 64$.
Soal No.20
Perbandingan panjang, lebar dan tinggi sebuah balok adalah $5:3:2$. Jika volume balok itu adalah $240$ cm3, maka luas permukaan balok tersebut adalah ... cm2
$ \begin{align} &(A). \ 62 \\ &(B). \ 124 \\ &(C). \ 182 \\ &(D). \ 218 \\ &(E). \ 248 \end{align} $
Perbandingan panjang, lebar dan tinggi sebuah balok adalah $5:3:2$. Jika volume balok itu adalah $240$ cm3, maka luas permukaan balok tersebut adalah ... cm2
$ \begin{align} &(A). \ 62 \\ &(B). \ 124 \\ &(C). \ 182 \\ &(D). \ 218 \\ &(E). \ 248 \end{align} $
Jenis soal macam ini caranya mudah, tinggal kita kasih pembanding aja perbandingannya.
Misal kasih pembanding $a$, sehingga :
\( p : l : t = 5a : 3a : 2a \)
$ \begin{align} V &= p \times l \times t \\ 240 &= 5a \times 3a \times 2a \\ 240 &= 30a^3 \\ 8 &= a^3 \to a=2 \end{align} $
$ \begin{align} L_p &= 2(pl+pt+lt) \\ &= 2(15a^2+10a^2+6a^2) \\ &= 62a^2 \\ \\ a &= 2 \to L_p = 62(4) =248 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 248$.
Misal kasih pembanding $a$, sehingga :
\( p : l : t = 5a : 3a : 2a \)
$ \begin{align} V &= p \times l \times t \\ 240 &= 5a \times 3a \times 2a \\ 240 &= 30a^3 \\ 8 &= a^3 \to a=2 \end{align} $
$ \begin{align} L_p &= 2(pl+pt+lt) \\ &= 2(15a^2+10a^2+6a^2) \\ &= 62a^2 \\ \\ a &= 2 \to L_p = 62(4) =248 \end{align} $
Jadi, jawaban yang BENAR adalah $(E). \ 248$.
Soal No.21
Diantara tabel di bawah ini yang menunjukkan hubungan perbandingan senilai adalah ...
HTML Table Generator
$(A.)$
$(B.)$
$(C.)$
$(D.)$
$(E.)$
Diantara tabel di bawah ini yang menunjukkan hubungan perbandingan senilai adalah ...
| $x$ | $2$ | $3$ | $8$ |
| $y$ | $8$ | $12$ | $24$ |
$(B.)$
| $x$ | $6$ | $10$ | $14$ |
| $y$ | $18$ | $30$ | $42$ |
$(C.)$
| $x$ | $2$ | $4$ | $6$ |
| $y$ | $12$ | $24$ | $36$ |
$(D.)$
| $x$ | $1$ | $3$ | $4$ |
| $y$ | $1$ | $9$ | $16$ |
$(E.)$
| $x$ | $1$ | $4$ | $5$ |
| $y$ | $1$ | $10$ | $25$ |
$
\begin{align}
\dfrac{2}{12} =\dfrac{4}{24} =\dfrac{6}{36}
\end{align}
$
Semua sebanding yaitu $1:6$.
Jadi, jawaban yang BENAR adalah $(C)$.
Semua sebanding yaitu $1:6$.
Jadi, jawaban yang BENAR adalah $(C)$.
Soal No.22
Jika $(3x+3):(6x-3)$ berbalik nilai dengan $(4x+1):(2x+4)$, nilai $x$ yang memenuhi adalah ...
$ \begin{align} &(A). \ 3 \\ &(B). \ 5 \\ &(C). \ 7 \\ &(D). \ 9 \\ &(E). \ 12 \end{align} $
Jika $(3x+3):(6x-3)$ berbalik nilai dengan $(4x+1):(2x+4)$, nilai $x$ yang memenuhi adalah ...
$ \begin{align} &(A). \ 3 \\ &(B). \ 5 \\ &(C). \ 7 \\ &(D). \ 9 \\ &(E). \ 12 \end{align} $
$
\begin{align}
\dfrac{(3x+3)}{(6x-3)} &= \dfrac{(2x+4)}{(4x+1)} \\ \\
(3x+3)(4x+1) &= (6x-3)(2x+4) \\
12x^{2}+15x+3 &= 12x^{2}+20x-12 \\
-5x &= -15 \\
x &= 3
\end{align}
$
Jadi, jawaban yang BENAR adalah $(A). \ 3$.
Jadi, jawaban yang BENAR adalah $(A). \ 3$.
Soal No.23
Jika $x:y=5:3$ dan $4x-3y=44$ maka nilai dari $x+2y-10$ adalah ...
$ \begin{align} &(A). \ 13 \\ &(B). \ 25 \\ &(C). \ 27 \\ &(D). \ 34 \\ &(E). \ 36 \end{align} $
Jika $x:y=5:3$ dan $4x-3y=44$ maka nilai dari $x+2y-10$ adalah ...
$ \begin{align} &(A). \ 13 \\ &(B). \ 25 \\ &(C). \ 27 \\ &(D). \ 34 \\ &(E). \ 36 \end{align} $
$
\begin{align}
\dfrac{x}{y} = \dfrac{5}{3} \to x &= \dfrac{5}{3}y \\ \\
4x-3y &= 44 \\
4 \left( \dfrac{5}{3}y \right)-3y &= 44 \\
\dfrac{11}{3}y &= 44 \\
y &= 12 \\ \\
x = \dfrac{5}{3}(12) \to x &= 20 \\ \\
x+2y-10 &= 20 + 24 -10 \\
&= 34
\end{align}
$
Jadi, jawaban yang BENAR adalah $(D). \ 34$.
Jadi, jawaban yang BENAR adalah $(D). \ 34$.
Soal No.24
Diketahui $m:n=3:4$. Hasil dari $(6m+n):(4m+5n)$ adalah ...
$ \begin{align} &(A). \ 1:2 \\ &(B). \ 1:3 \\ &(C). \ 3:5 \\ &(D). \ 7:8 \\ &(E). \ 11:16 \end{align} $
Diketahui $m:n=3:4$. Hasil dari $(6m+n):(4m+5n)$ adalah ...
$ \begin{align} &(A). \ 1:2 \\ &(B). \ 1:3 \\ &(C). \ 3:5 \\ &(D). \ 7:8 \\ &(E). \ 11:16 \end{align} $
$
\begin{align}
\dfrac{m}{n} = \dfrac{3}{4} \to m &= \dfrac{3}{4}n \\ \\
\dfrac{6m+n}{4m+5n} &= \dfrac{6 \left( \dfrac{3}{4}n \right)+n}{4 \left( \dfrac{3}{4}n \right)+5n} \\
&= \dfrac{\frac{22}{4}}{8} = \dfrac{11}{16}
\end{align}
$
Jadi, jawaban yang BENAR adalah $(E). \ 11:16$.
Jadi, jawaban yang BENAR adalah $(E). \ 11:16$.
Soal No.25
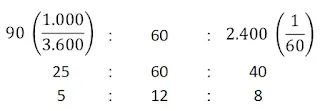
Bentuk sederhana dari $90$ km/jam $:$ $60$ m/detik $:$ $2.400$ m/menit adalah ...
$ \begin{align} &(A). \ 5:2:3 \\ &(B). \ 5:3:2 \\ &(C). \ 2:5:3 \\ &(D). \ 5:4:6 \\ &(E). \ 5:12:8 \end{align} $
Bentuk sederhana dari $90$ km/jam $:$ $60$ m/detik $:$ $2.400$ m/menit adalah ...
$ \begin{align} &(A). \ 5:2:3 \\ &(B). \ 5:3:2 \\ &(C). \ 2:5:3 \\ &(D). \ 5:4:6 \\ &(E). \ 5:12:8 \end{align} $
Untuk mengerjakan soal ini, caranya kita samakan semua satuannya menjadi dalam meter per detik.
Ingat !!!
$1$ km $= 1.000$ m
$1$ jam $=3.600$ detik
$1$ menit $= 60 $ detik
Sehingga
Jadi, jawaban yang BENAR adalah $(E). \ 5:12:8$.
Ingat !!!
$1$ km $= 1.000$ m
$1$ jam $=3.600$ detik
$1$ menit $= 60 $ detik
Sehingga
Soal No.26
Sebuah pesawat terbang panjang sayapnya adalah $50$ meter. Pada model berskala, panjang sayapnya adalah $20$ cm dan panjang badannya $60$ cm. Panjang badan pesawat tersebut sebenarnya adalah ... meter
$ \begin{align} &(A). \ 120 \\ &(B). \ 130 \\ &(C). \ 140 \\ &(D). \ 150 \\ &(E). \ 160 \end{align} $
Sebuah pesawat terbang panjang sayapnya adalah $50$ meter. Pada model berskala, panjang sayapnya adalah $20$ cm dan panjang badannya $60$ cm. Panjang badan pesawat tersebut sebenarnya adalah ... meter
$ \begin{align} &(A). \ 120 \\ &(B). \ 130 \\ &(C). \ 140 \\ &(D). \ 150 \\ &(E). \ 160 \end{align} $
$50$ m $=5.000$ cm
$ \begin{align} \dfrac{5.000}{x} &= \dfrac{20}{60} \\ \\ x &= 15.000 \ \text{cm} \\ &= 150 \ \text{m} \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 150$.
$ \begin{align} \dfrac{5.000}{x} &= \dfrac{20}{60} \\ \\ x &= 15.000 \ \text{cm} \\ &= 150 \ \text{m} \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 150$.
Soal No.27
Suatu pekerjaan dpat diselesaikan oleh $15$ orang pekerja dalam $2$ minggu. Jika pekerjaan itu akan diselesaikan dalam waktu $10$ hari maka banyaknya tambahan pekerja adalah ... orang
$ \begin{align} &(A). \ 5 \\ &(B). \ 6 \\ &(C). \ 8 \\ &(D). \ 14 \\ &(E). \ 21 \end{align} $
Suatu pekerjaan dpat diselesaikan oleh $15$ orang pekerja dalam $2$ minggu. Jika pekerjaan itu akan diselesaikan dalam waktu $10$ hari maka banyaknya tambahan pekerja adalah ... orang
$ \begin{align} &(A). \ 5 \\ &(B). \ 6 \\ &(C). \ 8 \\ &(D). \ 14 \\ &(E). \ 21 \end{align} $
CARA CEPAT!!!
$ \begin{align} \dfrac{21 \times 42}{21 + 42} &= \dfrac{882}{63} \\ &= 14 \ \text{jam} \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 14$.
$ \begin{align} \dfrac{21 \times 42}{21 + 42} &= \dfrac{882}{63} \\ &= 14 \ \text{jam} \end{align} $
Jadi, jawaban yang BENAR adalah $(D). \ 14$.
Soal No.28
Sari dan Ratih memiliki suatu pekerjaan yang sama dibidang fashion. Waktu yang dibutuhkan Sari dalam menyelesaikan pekerjaannya adalah $21$ jam, sedangkan Ratih butuh $42$ jam. Jika Sari dan Ratih bekerja bersama - sama untuk menyelesaikan pekerjaannya, waktu yang dibutuhkan adalah ... jam
$ \begin{align} &(A). \ 14 \\ &(B). \ 21 \\ &(C). \ 28 \\ &(D). \ 35 \\ &(E). \ 42 \end{align} $
Sari dan Ratih memiliki suatu pekerjaan yang sama dibidang fashion. Waktu yang dibutuhkan Sari dalam menyelesaikan pekerjaannya adalah $21$ jam, sedangkan Ratih butuh $42$ jam. Jika Sari dan Ratih bekerja bersama - sama untuk menyelesaikan pekerjaannya, waktu yang dibutuhkan adalah ... jam
$ \begin{align} &(A). \ 14 \\ &(B). \ 21 \\ &(C). \ 28 \\ &(D). \ 35 \\ &(E). \ 42 \end{align} $
$2$ minggu $=14$ hari
$ \begin{align} \dfrac{15}{10} &= \dfrac{x}{14} \\ \\ x &= \dfrac{15 \times 14}{10} \\ &= 21 \ \text{hari} \end{align} $
Jadi, jawaban yang BENAR adalah $(B). \ 21$.
$ \begin{align} \dfrac{15}{10} &= \dfrac{x}{14} \\ \\ x &= \dfrac{15 \times 14}{10} \\ &= 21 \ \text{hari} \end{align} $
Jadi, jawaban yang BENAR adalah $(B). \ 21$.
Soal No.29
Andri dapat menyelesaikan pekerjaan mendekorasi ruang tamu dalam $3$ hari, sedangkan Toni dapat menyelesaikan jenis pekerjaan yang sama dalam waktu $6$ hari. Jika mereka berdua bekerja sama maka waktu yang dibutuhkan adalah ... hari
$ \begin{align} &(A). \ 2 \\ &(B). \ 4 \\ &(C). \ 5 \\ &(D). \ 8 \\ &(E). \ 10 \end{align} $
Andri dapat menyelesaikan pekerjaan mendekorasi ruang tamu dalam $3$ hari, sedangkan Toni dapat menyelesaikan jenis pekerjaan yang sama dalam waktu $6$ hari. Jika mereka berdua bekerja sama maka waktu yang dibutuhkan adalah ... hari
$ \begin{align} &(A). \ 2 \\ &(B). \ 4 \\ &(C). \ 5 \\ &(D). \ 8 \\ &(E). \ 10 \end{align} $
CARA CEPAT!!!
$ \begin{align} \dfrac{3 \times 6}{3 + 6} &= \dfrac{18}{9} \\ &= 2 \ \text{hari} \end{align} $
Jadi, jawaban yang BENAR adalah $(A). \ 2$.
$ \begin{align} \dfrac{3 \times 6}{3 + 6} &= \dfrac{18}{9} \\ &= 2 \ \text{hari} \end{align} $
Jadi, jawaban yang BENAR adalah $(A). \ 2$.
Soal No.30
Perbandingan volume bola yang berjari - jari $5$ cm dan tabung yang alasnya berjari - jari sama namun tingginya $10$ cm adalah ...
$ \begin{align} &(A). \ 1:2 \\ &(B). \ 2:3 \\ &(C). \ 3:4 \\ &(D). \ 4:5 \\ &(E). \ 5:6 \end{align} $
Perbandingan volume bola yang berjari - jari $5$ cm dan tabung yang alasnya berjari - jari sama namun tingginya $10$ cm adalah ...
$ \begin{align} &(A). \ 1:2 \\ &(B). \ 2:3 \\ &(C). \ 3:4 \\ &(D). \ 4:5 \\ &(E). \ 5:6 \end{align} $
$
\begin{align}
\dfrac{V_{\text{Bola}}}{V_{\text{Tabung}}} &= \dfrac{\dfrac{4}{3} \times \pi \times 5^{3} }{\pi \times 5^{2} \times 10} \\ \\
\dfrac{V_{\text{Bola}}}{V_{\text{Tabung}}} &= \dfrac{500}{750} = \dfrac{2}{3}
\end{align}
$
Jadi, jawaban yang BENAR adalah $(B). \ 2:3$.
Jadi, jawaban yang BENAR adalah $(B). \ 2:3$.
Penutup
Nah, gimana?Udah mulai paham soal perbandingan, kan?
Ingat, kunci sukses nguasain materi ini adalah sering latihan dan nggak takut salah.
Semoga artikel ini bantu kamu lebih siap menghadapi ujian.
Jangan lupa bahagia dan jaga belajar ya.
Tetap semangat belajar ya!😊
"Belajar adalah jembatan untuk mencapai impian. Jangan pernah berhenti belajar, karena kehidupan tak pernah berhenti mengajarkan." – Anonim
