Model Soal Terbaru Pengetahuan Kuantitatif UTBK SNBT 2025 Hari Pertama Sampai Akhir
Ini adalah kumpulan soal model terbaru yang katanya keluar pada UTBK SNBT 2025, update mulai dari hari pertama sampai hari terakhir dilaksanakan.
Momen penyelenggaraan UTBK SNBT 2025 baru saja berakhir pada Sabtu 3 Mei 2025 kemarin.
Soal - soal yang di_klaim katanya bocor dari naskah asli yang keluar, santer menjadi perbincangan dan incaran publik beberapa hari kemarin.
Yah.. lagi - lagi kecurangan masih saja terjadi, sungguh sangat disayangkan.
Jadi, buat kamu - kamu yang akan join tes UTBK SNBT tahun depan, beberapa materi dibawah ini bisa buat catatan target belajar agar nilai sub tes pengetahuan kuantitatifmu maksimal.
Beberapa materi soal pengetahuan kuantitatif yang keluar pada UTBK SNBT 2025 adalah :
Pelan - pelan aja mahaminnya, jangan lupa sebelum lihat dan nyimak pembahasannya lebih baik cobain mengerjakan soalnya dulu ya.
Practice makes perfect!!!🔥🔥🔥
Rasanya kayak lagi main game level expert, tapi tenang ... setiap soal yang kamu kerjain itu bikin “level otak” naik terus.
Belajar UTBK tuh nggak harus tegang terus kayak nunggu ditembak sama dia hehe...
Santai, tapi serius. Capek boleh, nyerah jangan!
Ingat kata Goku di Dragon Ball Z,
"Power comes in response to a need, not a desire. You have to create that need."
Artinya? Kalau kamu ngerasa UTBK itu penting, otakmu bakal auto nyari cara buat ngerti, asal kamu mau mulai dulu.
Jadi, yuk terus belajar, latihan soal, dan jangan lupa jaga mental biar tetap waras. UTBK itu bukan boss terakhir hidup kamu, tapi tetep harus ditaklukin buat naik ke level selanjutnya.
Semangat, Pejuang SNBT 2026! Kalo karakter anime bisa ngeluarin jurus pamungkas pas kepepet, kamu juga bisa kok ngeluarin usaha maksimal pas ujian! 🎮📚🔥
Momen penyelenggaraan UTBK SNBT 2025 baru saja berakhir pada Sabtu 3 Mei 2025 kemarin.
Soal - soal yang di_klaim katanya bocor dari naskah asli yang keluar, santer menjadi perbincangan dan incaran publik beberapa hari kemarin.
Yah.. lagi - lagi kecurangan masih saja terjadi, sungguh sangat disayangkan.
Bab - Bab Yang Keluar di Pengetahuan Kuantitatif
Berkaca dari pelaksanaan UTBK SNBT 2025 beberapa materi yang keluar sebenarnya sebagian besar hampir tidak berubah dari bab atau materi yang keluar pada tiga tahun terakhir.Jadi, buat kamu - kamu yang akan join tes UTBK SNBT tahun depan, beberapa materi dibawah ini bisa buat catatan target belajar agar nilai sub tes pengetahuan kuantitatifmu maksimal.
Beberapa materi soal pengetahuan kuantitatif yang keluar pada UTBK SNBT 2025 adalah :
- Operasi Bilangan
- Himpunan
- Relasi dan Fungsi
- Persamaan dan Fungsi Kuadrat
- Persamaan Garis dan Gradien
- Barisan dan Deret
- Pertidaksamaan
- Trigonometri
- Bangun Ruang dan Bangun Datar
- Kombinatorika dan Peluang
- Statistika
10 Tips Ngerjain Soal Pengetahuan Kuantitatif UTBK dengan Mudah dan Cepat
Tips - tips jitu di bawah ini bisa ngebantu kamu buat ngerjain soal - soal pengetahuan kuantitatif UTBK dengan mudah dan cepat.- Pahami Konsep Dasar, Jangan Hafal Rumus Doang
- Latihan Soal Tiap Hari Walau Sedikit
- Gunakan Logika dan Estimasi
- Hafalin Angka-Angka Penting
- Kerjakan Soal Mudah Dulu
- Gunakan Strategi Backsolving
- Kenali Tipe Soal yang Sering Keluar
- Bikin Catatan “Rumus Pintar” atau “Rumus Cepat”
- Simulasi UTBK Minimal 1 Kali Seminggu
Paham konsep akan jauh lebih baik daripada hanya hafal rumus doang. Daripada hafal rumus volume tabung $V= \pi r^2 t$ mending paham bahwa "volume tabung itu adalah luas alas kali tinggi".
Konsisten lebih penting daripada maraton. Coba targetin minimal 5 soal kuantitatif per hari, nanti lama-lama kamu bakal ngebentuk insting matematika kamu.
Kadang soal bisa diselesaikan pakai nalar logika tanpa hitung ribet. Misalnya soal perbandingan, kadang cukup pakai logika "oh ini lebih besar 2x dari itu".
Seperti : Kuadrat 1–20, akar kuadrat penting (√2 ≈ 1,41, √3 ≈ 1,73), faktorisasi prima. Ini ngebantu banget buat hitungan cepat tanpa kalkulator.
Di UTBK, waktu itu emas. Kerjain soal yang kamu bisa duluan. Lewatin yang ribet, nanti balik lagi kalau ada waktu. Jangan kejebak satu soal terlalu lama.
Ini teknik “coba-coba” dari pilihan jawaban. Misalnya kamu nggak bisa ngerjain aljabar secara formal, masukin aja pilihan A, B, C ke soalnya dan lihat mana yang cocok.
Coba catet dan tandai tipe soal yang sering keluar dari tahun - tahun sebelumnya. Itu bisa jadi acuan.
Tulis rumus atau trik-trik cepat versi kamu sendiri. Misalnya Seperti : “Jika ada kata 'paling sedikit' = berarti pakai pertidaksamaan lebih dari”. Catatan pribadi itu bikin otak kamu lebih nempel karena kamu sendiri yang nyusun.
Ini nih yang sering dilupakan. Biasakan diri sama waktu dan tekanan. Set timer, kerjain soal TPS beneran, jangan buka catatan. Abis itu evaluasi: soal mana yang makan waktu banyak, mana yang salah. Bisa juga kamu join TOBK daring, ngga harus yang berbayar. Gratisan banyak.
Soal Terbaru Pengetahuan Kuantitatif UTBK SNBT 2025
Beberapa soal di bawah ini diklaim katanya keluar di sub tes Pengetahuan Kuantitatif UTBK 2025 hari pertama sampai hari akhir pelaksanaan tanggal 3 Mei 2025.Pelan - pelan aja mahaminnya, jangan lupa sebelum lihat dan nyimak pembahasannya lebih baik cobain mengerjakan soalnya dulu ya.
Practice makes perfect!!!🔥🔥🔥
Soal No.1
Titik $R(5,-4)$ terletak pada grafik $y = 3x^2 + rx - 44$ maka nilai $r$ adalah..
$ \begin{align} & (A). -15 \\ & (B). -7 \\ & (C). 4 \\ & (D). 7 \\ & (E). 15 \end{align} $
Titik $R(5,-4)$ terletak pada grafik $y = 3x^2 + rx - 44$ maka nilai $r$ adalah..
$ \begin{align} & (A). -15 \\ & (B). -7 \\ & (C). 4 \\ & (D). 7 \\ & (E). 15 \end{align} $
Kamu cukup substitusikan titik $R(5,-4)$ pada fungsinya untuk menyelesaikan soal ini.
$ \begin{align} y &= 3x^2 + rx - 44 \\ -4 &= 3(5)^2 + r(5) - 44 \\ -4 &= 75 + 5r - 44 \\ -35 &= 5r \\ r &= -7 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). -7$.
$ \begin{align} y &= 3x^2 + rx - 44 \\ -4 &= 3(5)^2 + r(5) - 44 \\ -4 &= 75 + 5r - 44 \\ -35 &= 5r \\ r &= -7 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). -7$.
Soal No.2
Jika $5 : \dfrac{1}{3}= \sqrt{t}$ maka nilai $t=$ ...
$ \begin{align} & (A). 121 \\ & (B). 169 \\ & (C). 196 \\ & (D). 225 \\ & (E). 625 \end{align} $
Jika $5 : \dfrac{1}{3}= \sqrt{t}$ maka nilai $t=$ ...
$ \begin{align} & (A). 121 \\ & (B). 169 \\ & (C). 196 \\ & (D). 225 \\ & (E). 625 \end{align} $
Ngga usah overthinking, asli mudah kok soal ini. Kamu pasti bisa !
$ \begin{align} 5 : \dfrac{1}{3} &= \sqrt{t} \\ 15 &= \sqrt{t} \ \ \text{| kuadratkan kedua ruas}\\ 225 &= t \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 225$.
$ \begin{align} 5 : \dfrac{1}{3} &= \sqrt{t} \\ 15 &= \sqrt{t} \ \ \text{| kuadratkan kedua ruas}\\ 225 &= t \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 225$.
Soal No.3
Fungsi $f$ didefinisikan dengan $f(x)=x^2-3x$. Nilai $\dfrac{f(f(f(2)))}{f(f(2))}-f(2)$ adalah ...
Fungsi $f$ didefinisikan dengan $f(x)=x^2-3x$. Nilai $\dfrac{f(f(f(2)))}{f(f(2))}-f(2)$ adalah ...
$
\begin{align}
f(x) &= x^2-3x
\end{align}
$
$ \begin{align} f(2) &= 2^2-3(2) \\ &= -2 \end{align} $
$ \begin{align} f(-2) &= (-2)^2-3(-2) \\ &= 10 \end{align} $
$ \begin{align} f(10) &= 10^2-3(10) \\ &= 70 \end{align} $
$ \begin{align} \dfrac{f(f(f(2)))}{f(f(2))}-f(2) &= \dfrac{f(f(-2))}{f(-2)}-(-2) \\ &= \dfrac{f(10)}{10}-(-2) \\ &= \dfrac{70}{10}-(-2) \\ &= 9 \end{align} $
Jadi, jawaban soal ini adalah $9$.
$ \begin{align} f(2) &= 2^2-3(2) \\ &= -2 \end{align} $
$ \begin{align} f(-2) &= (-2)^2-3(-2) \\ &= 10 \end{align} $
$ \begin{align} f(10) &= 10^2-3(10) \\ &= 70 \end{align} $
$ \begin{align} \dfrac{f(f(f(2)))}{f(f(2))}-f(2) &= \dfrac{f(f(-2))}{f(-2)}-(-2) \\ &= \dfrac{f(10)}{10}-(-2) \\ &= \dfrac{70}{10}-(-2) \\ &= 9 \end{align} $
Jadi, jawaban soal ini adalah $9$.
Soal No.4
Diantara bilangan berikut yang merupakan faktor persekutuan dari $(49^2+49)$ dan $(12^2-2^2)$ sama dengan ...
$ \begin{array}{cc} (1) \ 10 & (3) \ 35 \\ (2) \ 14 & (4) \ 50 \\ \end{array} $
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
Diantara bilangan berikut yang merupakan faktor persekutuan dari $(49^2+49)$ dan $(12^2-2^2)$ sama dengan ...
$ \begin{array}{cc} (1) \ 10 & (3) \ 35 \\ (2) \ 14 & (4) \ 50 \\ \end{array} $
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
Cari dulu nilai dari kedua bilangannya :
$ \begin{align} (49^2+49) &= 2401 + 49 \\ &= 2450 \\ \\ (12^2-2^2) &= 144-4 \\ &= 140 \end{align} $
$10$, $14$ dan $35$ jelas faktor keduanya, karena $10$ bisa membagi habis $2450$ dan $142$.
$50$ bukanlah faktor keduanya, karena $50$ hanya bisa membagi habis $2450$ tapi tidak dengan $140$.
Jadi, pilihan jawaban yang TEPAT adalah $(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$ \begin{align} (49^2+49) &= 2401 + 49 \\ &= 2450 \\ \\ (12^2-2^2) &= 144-4 \\ &= 140 \end{align} $
$10$, $14$ dan $35$ jelas faktor keduanya, karena $10$ bisa membagi habis $2450$ dan $142$.
$50$ bukanlah faktor keduanya, karena $50$ hanya bisa membagi habis $2450$ tapi tidak dengan $140$.
Jadi, pilihan jawaban yang TEPAT adalah $(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
Soal No.5
Enam bilangan positif, yaitu $1$,$4$,$6$,$3$,$b$,$8$ memiliki rata - rata $b\dfrac{1}{3}$. Jika jangkauan dari keenam bilangan tersebut dikurangi rata - ratanya adalah $\dfrac{Q}{15}$, nilai $Q$ sama dengan ...
Enam bilangan positif, yaitu $1$,$4$,$6$,$3$,$b$,$8$ memiliki rata - rata $b\dfrac{1}{3}$. Jika jangkauan dari keenam bilangan tersebut dikurangi rata - ratanya adalah $\dfrac{Q}{15}$, nilai $Q$ sama dengan ...
Mulai dari nilai rata - ratanya kamu bisa dapatkan nilai $b$ nya.
$ \begin{align} \dfrac{1+4+6+3+b+8}{6} &= b\dfrac{1}{3} \\ \dfrac{22+b}{6} &= \dfrac{3b+1}{3} \\ 22+b &= 6b+2 \\ 20 &= 5b \to b=4 \end{align} $
Untuk mencari jangkauan ingat data wajib diurutkan dari terkecil ke terbesar.
Kita peroleh $1$,$3$,$4$,$4$,$6$,$8$.
$ \begin{align} J - \bar{x} &= \dfrac{Q}{15} \\ \left( 8-1 \right) - 4\dfrac{1}{3} &= \dfrac{Q}{15} \\ 7 - \dfrac{13}{3} &= \dfrac{Q}{15} \\ \dfrac{21-13}{3} &= \dfrac{Q}{15} \\ \dfrac{8}{3} &= \dfrac{Q}{15} \\ Q &= 40 \end{align} $
Jadi, nilai $Q$ jawaban soal ini adalah $40$.
$ \begin{align} \dfrac{1+4+6+3+b+8}{6} &= b\dfrac{1}{3} \\ \dfrac{22+b}{6} &= \dfrac{3b+1}{3} \\ 22+b &= 6b+2 \\ 20 &= 5b \to b=4 \end{align} $
Untuk mencari jangkauan ingat data wajib diurutkan dari terkecil ke terbesar.
Kita peroleh $1$,$3$,$4$,$4$,$6$,$8$.
$ \begin{align} J - \bar{x} &= \dfrac{Q}{15} \\ \left( 8-1 \right) - 4\dfrac{1}{3} &= \dfrac{Q}{15} \\ 7 - \dfrac{13}{3} &= \dfrac{Q}{15} \\ \dfrac{21-13}{3} &= \dfrac{Q}{15} \\ \dfrac{8}{3} &= \dfrac{Q}{15} \\ Q &= 40 \end{align} $
Jadi, nilai $Q$ jawaban soal ini adalah $40$.
Soal No.6
Fungsi $f$ dengan variabel real $x$ memenuhi
\[ 3^{x-1} \lt f(x) \lt 3x^2+1 \] untuk $x \le 4$.
Diantara pilihan berikut, nilai $f$ di $x=3$ yang TIDAK MUNGKIN adalah ...
$ \begin{array}{cc} (1) \ \ \ 7 & (3) \ \ \ 9 \\ (2) \ 12 & (4) \ 24 \\ \end{array} $
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
Fungsi $f$ dengan variabel real $x$ memenuhi
\[ 3^{x-1} \lt f(x) \lt 3x^2+1 \] untuk $x \le 4$.
Diantara pilihan berikut, nilai $f$ di $x=3$ yang TIDAK MUNGKIN adalah ...
$ \begin{array}{cc} (1) \ \ \ 7 & (3) \ \ \ 9 \\ (2) \ 12 & (4) \ 24 \\ \end{array} $
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
Untuk cek nilai mana aja yang TIDAK MUNGKIN caranya cukup simpel, kamu tinggal substitusikan aja nilai $x=3$ nya ke pertidaksamaannya.
$ \begin{align} 3^{x-1} &\lt f(x) \lt 3x^2+1 \\ x=3 \to 3^{3-1} &\lt f(3) \lt 3(3)^2+1 \\ 3^2 &\lt f(3) \lt 3(9)+1 \\ 9 &\lt f(3) \lt 28 \\ \end{align} $
Terlihat jelas bahwa nilai $f(3)$ terletak diantara $9$ dan $28$.
Sehingga nilai $f$ yang MUNGKIN hanya $24$.
Jadi, pilihan jawaban yang TEPAT adalah $(D).$ $(4)$ SAJA.
$ \begin{align} 3^{x-1} &\lt f(x) \lt 3x^2+1 \\ x=3 \to 3^{3-1} &\lt f(3) \lt 3(3)^2+1 \\ 3^2 &\lt f(3) \lt 3(9)+1 \\ 9 &\lt f(3) \lt 28 \\ \end{align} $
Terlihat jelas bahwa nilai $f(3)$ terletak diantara $9$ dan $28$.
Sehingga nilai $f$ yang MUNGKIN hanya $24$.
Jadi, pilihan jawaban yang TEPAT adalah $(D).$ $(4)$ SAJA.
Soal No.7
Untuk setiap bilangan bulat $x$, didefinisikan
$[x)=\begin{cases} \dfrac{x+3}{x-2}, & \mbox{jika x ganjil} \\ \\ \dfrac{x^2+2}{2}, & \mbox{jika x genap tak negatif} \\ \\ 2x^2+1, & \mbox{jika x genap negatif} \end{cases}$
Nilai $[1-[2))$ adalah ...
$ \begin{align} & (A). -7 \\ & (B). 3 \\ & (C). 4 \\ & (D). 5 \\ & (E). 9 \end{align} $
Untuk setiap bilangan bulat $x$, didefinisikan
$[x)=\begin{cases} \dfrac{x+3}{x-2}, & \mbox{jika x ganjil} \\ \\ \dfrac{x^2+2}{2}, & \mbox{jika x genap tak negatif} \\ \\ 2x^2+1, & \mbox{jika x genap negatif} \end{cases}$
Nilai $[1-[2))$ adalah ...
$ \begin{align} & (A). -7 \\ & (B). 3 \\ & (C). 4 \\ & (D). 5 \\ & (E). 9 \end{align} $
Kamu ngga usah bingung dengan model fungsi seperti ini, dalam matematika ini yang disebut dengan fungsi tangga.
Cara mengerjakannya kamu tinggal pilih fungsinya berdasarkan nilai $x$ yang akan dipakai.
Kita cari dulu $[2)$, karena $2$ adalah bilangan genap tak negatif maka kita pilih fungsi $\dfrac{x^2+2}{2}$.
Sehingga kita peroleh,
$ \begin{align} \dfrac{x^2+2}{2} &= \dfrac{2^2+2}{2} \\ &= \dfrac{6}{2} = 3 \end{align} $
Dengan demikian $[1-[2)) = [1-3)=[-2)$, karena $-2$ bilangan genap negatif maka kita akan substitusikan ke fungsi yang ketiga yaitu $2x^2+1$.
Kita peroleh,
$ \begin{align} 2x^2+1 &= 2(-2)^2+1 \\ &= 9 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E). 9$.
Cara mengerjakannya kamu tinggal pilih fungsinya berdasarkan nilai $x$ yang akan dipakai.
Kita cari dulu $[2)$, karena $2$ adalah bilangan genap tak negatif maka kita pilih fungsi $\dfrac{x^2+2}{2}$.
Sehingga kita peroleh,
$ \begin{align} \dfrac{x^2+2}{2} &= \dfrac{2^2+2}{2} \\ &= \dfrac{6}{2} = 3 \end{align} $
Dengan demikian $[1-[2)) = [1-3)=[-2)$, karena $-2$ bilangan genap negatif maka kita akan substitusikan ke fungsi yang ketiga yaitu $2x^2+1$.
Kita peroleh,
$ \begin{align} 2x^2+1 &= 2(-2)^2+1 \\ &= 9 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E). 9$.
Soal No.8
Jika $0^{\circ} \lt \alpha \lt 90^{\circ}$ dan $\cos {\alpha}=\dfrac{3}{4}$, diantara beberapa pernyataan di bawah ini yang BENAR adalah ...
(1) $\sin {\alpha}=\dfrac{4}{\sqrt{7}}$
(2) $\tan \left( 90^{\circ}-\alpha \right) =\dfrac{3}{\sqrt{7}}$
(3) $\cos {\alpha} \lt \sin {\alpha}$
(4) $\tan {\alpha}=\dfrac{\sqrt{7}}{3}$
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
Jika $0^{\circ} \lt \alpha \lt 90^{\circ}$ dan $\cos {\alpha}=\dfrac{3}{4}$, diantara beberapa pernyataan di bawah ini yang BENAR adalah ...
(1) $\sin {\alpha}=\dfrac{4}{\sqrt{7}}$
(2) $\tan \left( 90^{\circ}-\alpha \right) =\dfrac{3}{\sqrt{7}}$
(3) $\cos {\alpha} \lt \sin {\alpha}$
(4) $\tan {\alpha}=\dfrac{\sqrt{7}}{3}$
$(A).$ $(1)$, $(2)$, dan $(3)$ SAJA.
$(B).$ $(1)$ dan $(3)$ SAJA.
$(C).$ $(2)$ dan $(4)$ SAJA.
$(D).$ $(4)$ SAJA.
$(E).$ SEMUA benar.
$0^{\circ} \lt \alpha \lt 90^{\circ}$ artinya $\alpha$ terletak pada kuadran I, sehingga semua nilai fungsi trigonometrinya ($\sin \alpha$, $\cos \alpha$, $\tan \alpha$, dst ...) akan bernilai positif.
Cara paling mudah mengerjakan soal ini tentu saja kamu bisa pakai perbandingan pada segitiga siku - siku.
Sehingga,
Cara paling mudah mengerjakan soal ini tentu saja kamu bisa pakai perbandingan pada segitiga siku - siku.
Sehingga,
- $\sin \alpha = \dfrac{\sqrt{7}}{4}$ (Salah)
- $\tan \left( 90^{\circ}-\alpha \right)=\tan {\alpha}=\dfrac{\sqrt{7}}{3}$ (Salah)
- $\cos {\alpha} \lt \sin {\alpha}$ (Salah)
- $\tan {\alpha}=\dfrac{\sqrt{7}}{3}$ (Benar)
Soal No.9
Grafik fungsi $f(x)=2x^2-x-1$ dan $g(x)=x^2-3x+7$ berpotongan di dua titik berbeda, yaitu $K(a,b)$ dan $L(c,d)$. Sebuah garis $m$ melalui kedua titik tersebut. Gradien garis $m$ sama dengan ...
$ \begin{align} & (A). -5 \\ & (B). -\dfrac{1}{5} \\ & (C). 1 \\ & (D). \dfrac{1}{5} \\ & (E). 5 \end{align} $
Grafik fungsi $f(x)=2x^2-x-1$ dan $g(x)=x^2-3x+7$ berpotongan di dua titik berbeda, yaitu $K(a,b)$ dan $L(c,d)$. Sebuah garis $m$ melalui kedua titik tersebut. Gradien garis $m$ sama dengan ...
$ \begin{align} & (A). -5 \\ & (B). -\dfrac{1}{5} \\ & (C). 1 \\ & (D). \dfrac{1}{5} \\ & (E). 5 \end{align} $
Titik potong kedua kurva,
$ \begin{align} f(x) &= g(x) \\ 2x^2-x-1 &= x^2-3x+7 \\ x^2+2x-8 &= 0 \\ (x+4)(x-2) &= 0 \\ x=-4 \ \text{atau} \ x&=2 \end{align} $
$ \begin{align} x=-4 \ \to \ y &= (-4)^2-3(-4)+7 \\ y &= 35 \\ \\ x=2 \ \to \ y &= (2)^2-3(2)+7 \\ y &= 5 \end{align} $
Kita dapatkan $K(-4,35)$ dan $L(2,5)$ atau sebaliknya.
Gradien garis yang melalui kedua titik $K$ dan $L$ adalah,
$ \begin{align} m &= \dfrac{y_2-y_1}{x_2-x_1} \\ m &= \dfrac{35-5}{-4-2} \\ m &= -5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A). -5 $
$ \begin{align} f(x) &= g(x) \\ 2x^2-x-1 &= x^2-3x+7 \\ x^2+2x-8 &= 0 \\ (x+4)(x-2) &= 0 \\ x=-4 \ \text{atau} \ x&=2 \end{align} $
$ \begin{align} x=-4 \ \to \ y &= (-4)^2-3(-4)+7 \\ y &= 35 \\ \\ x=2 \ \to \ y &= (2)^2-3(2)+7 \\ y &= 5 \end{align} $
Kita dapatkan $K(-4,35)$ dan $L(2,5)$ atau sebaliknya.
Gradien garis yang melalui kedua titik $K$ dan $L$ adalah,
$ \begin{align} m &= \dfrac{y_2-y_1}{x_2-x_1} \\ m &= \dfrac{35-5}{-4-2} \\ m &= -5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A). -5 $
Soal No.10
Sebuah barisan aritmatika $a_1, a_2,a_3, \cdot$ memiliki suku - suku yang bulat dan selisih diantara dua suku yang berurutan $-3$.
Apakah $a_{2025}$ genap?
Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.
(1) $a_1 + a_2$ ganjil.
(2) $a_2 + a_3$ ganjil.
Sebuah barisan aritmatika $a_1, a_2,a_3, \cdot$ memiliki suku - suku yang bulat dan selisih diantara dua suku yang berurutan $-3$.
Apakah $a_{2025}$ genap?
Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.
(1) $a_1 + a_2$ ganjil.
(2) $a_2 + a_3$ ganjil.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA- SAMA cukup untuk menjawab pertanyaan, tetapi SATU pertanyaan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Soal No.11
Sembilan bilangan $2,$$4,$$8,$$3,$$6,$$5,$$7,$$8,$$4$ diurutkan dari yang terbesar hingga ke terkecil. Jika $u$ dan $t$ merepresentasikan bilangan posisi ke-$3$ dan ke-$8$ setelah diurutkan maka nilai $\left(2 \times u \right)-t$ adalah ...
$ \begin{align} & (A). 14 \\ & (B). 13 \\ & (C). 12 \\ & (D). 11 \\ & (E). 10 \end{align} $
Sembilan bilangan $2,$$4,$$8,$$3,$$6,$$5,$$7,$$8,$$4$ diurutkan dari yang terbesar hingga ke terkecil. Jika $u$ dan $t$ merepresentasikan bilangan posisi ke-$3$ dan ke-$8$ setelah diurutkan maka nilai $\left(2 \times u \right)-t$ adalah ...
$ \begin{align} & (A). 14 \\ & (B). 13 \\ & (C). 12 \\ & (D). 11 \\ & (E). 10 \end{align} $
Kita urutkan bilangannya dari terbesar ke terkecil,
\[ 8,8,7,6,5,4,4,3,2 \]
Sehingga, $u=7$ dan $t=3$.
Dengan demikian,
$ \begin{align} \left(2 \times u \right)-t &= \left(2 \times 7 \right)-3 \\ &= 14-3 =11 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 11 $.
Dengan demikian,
$ \begin{align} \left(2 \times u \right)-t &= \left(2 \times 7 \right)-3 \\ &= 14-3 =11 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 11 $.
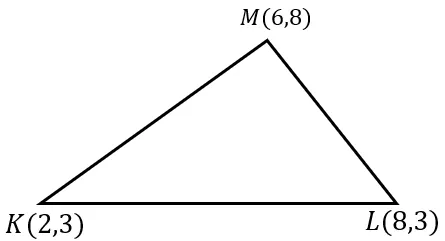
Soal No.12
Suatu limas dengan volume $30$ memiliki alas berupa daerah segitiga $KLM$. Koordinat $K(2,3)$, $L(8,3)$ dan $M(6,8)$ seperti nampak pada gambar berikut.
Jarak antara titik $M$ dan sisi $KL$ adalah ...
$ \begin{align} & (A). \sqrt{41} \\ & (B). 6 \\ & (C). \sqrt{29} \\ & (D). 5 \\ & (E). 3 \end{align} $
Suatu limas dengan volume $30$ memiliki alas berupa daerah segitiga $KLM$. Koordinat $K(2,3)$, $L(8,3)$ dan $M(6,8)$ seperti nampak pada gambar berikut.
Jarak antara titik $M$ dan sisi $KL$ adalah ...
$ \begin{align} & (A). \sqrt{41} \\ & (B). 6 \\ & (C). \sqrt{29} \\ & (D). 5 \\ & (E). 3 \end{align} $
Cara (1) :
Jarak sebuah titik $(x_1,y_1)$ terhadap garis $Ax+By+C=0$ adalah \[ \left| \dfrac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right| \] Persamaan garis yang melalui $KL$,
$ \begin{align} \dfrac{y-y_1}{y_2-y_1} &= \dfrac{x-x_1}{x_2-x_1} \\ \dfrac{y-3}{3-3} &= \dfrac{x-2}{8-2} \\ \dfrac{y-3}{0} &= \dfrac{x-2}{6} \ \text{| kalikan silang}\\ 6y-18 &= 0 \\ y &= 3 \end{align} $
Dengan demikian jarak titik $M(6,8)$ terhadap garis $y=3$ adalah,
$ \begin{align} \left| \dfrac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right| &= \left| \dfrac{0(6)+1(8)-3}{\sqrt{0^2+1^2}} \right| \\ &= \left| \dfrac{5}{\sqrt{1}} \right| = 5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 5 $.
Cara (2) : CARA CEPAT!!!
Karena $KL$ sejajar dengan sumbu-$X$ maka menghitung jarak $M$ ke $KL$ cukup mencari selisih ordinat($y$) pada kedua titik.
Kita ambil nilai ordinat pada titik $M(6,8)$ yaitu $8$ dan titik $L(8,3)$ yaitu $3$.
Sehingga jarak jarak $M$ ke $KL$ adalah $8-3=5$
Jadi, pilihan jawaban yang TEPAT adalah $(D). 5 $.
Jarak sebuah titik $(x_1,y_1)$ terhadap garis $Ax+By+C=0$ adalah \[ \left| \dfrac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right| \] Persamaan garis yang melalui $KL$,
$ \begin{align} \dfrac{y-y_1}{y_2-y_1} &= \dfrac{x-x_1}{x_2-x_1} \\ \dfrac{y-3}{3-3} &= \dfrac{x-2}{8-2} \\ \dfrac{y-3}{0} &= \dfrac{x-2}{6} \ \text{| kalikan silang}\\ 6y-18 &= 0 \\ y &= 3 \end{align} $
Dengan demikian jarak titik $M(6,8)$ terhadap garis $y=3$ adalah,
$ \begin{align} \left| \dfrac{Ax_1+By_1+C}{\sqrt{A^2+B^2}} \right| &= \left| \dfrac{0(6)+1(8)-3}{\sqrt{0^2+1^2}} \right| \\ &= \left| \dfrac{5}{\sqrt{1}} \right| = 5 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 5 $.
Cara (2) : CARA CEPAT!!!
Karena $KL$ sejajar dengan sumbu-$X$ maka menghitung jarak $M$ ke $KL$ cukup mencari selisih ordinat($y$) pada kedua titik.
Kita ambil nilai ordinat pada titik $M(6,8)$ yaitu $8$ dan titik $L(8,3)$ yaitu $3$.
Sehingga jarak jarak $M$ ke $KL$ adalah $8-3=5$
Jadi, pilihan jawaban yang TEPAT adalah $(D). 5 $.
Soal No.13
Sebuah barisan mempunyai suku - suku $a_1,$$a_2,$$a_3,$$\cdot$$a_n,$. Barisan tersebut memenuhi $a_n=a_{n-1}+4$ dan $a_7=-2$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
HTML Table Generator
Sebuah barisan mempunyai suku - suku $a_1,$$a_2,$$a_3,$$\cdot$$a_n,$. Barisan tersebut memenuhi $a_n=a_{n-1}+4$ dan $a_7=-2$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
| $a_{15}$ | $31$ |
- Kuantitas $P$ lebih dari $Q$.
- Kuantitas $P$ kurang dari $Q$.
- Kuantitas $P$ sama dengan $Q$.
- Tidak dapat ditentukan hubungan kuantitas $P$ dan $Q$.
Soal No.14
Segitiga $ABC$ merupakan segitiga sama sisi dengan panjang sisi $4$. Daerah segitiga $ABC$ memiliki luas $L_1$. Titik $D$ merupakan titik tengah $AB$ dan titik $E$ berada di ruas garis $CD$ sehingga luas segitiga $ABE$ adalah $L_2$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
HTML Table Generator
Segitiga $ABC$ merupakan segitiga sama sisi dengan panjang sisi $4$. Daerah segitiga $ABC$ memiliki luas $L_1$. Titik $D$ merupakan titik tengah $AB$ dan titik $E$ berada di ruas garis $CD$ sehingga luas segitiga $ABE$ adalah $L_2$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
| $\dfrac{1}{3}$ | $\dfrac{L_2}{L_1}$ |
- Kuantitas $P$ lebih dari $Q$.
- Kuantitas $P$ kurang dari $Q$.
- Kuantitas $P$ sama dengan $Q$.
- Tidak dapat ditentukan hubungan kuantitas $P$ dan $Q$.
Soal No.15
Banyaknya persegi pada bangun datar (diagram kartesius) di bawah ini adalah ...
$ \begin{align} & (A). 8 \\ & (B). 10 \\ & (C). 12 \\ & (D). 14 \\ & (E). 20 \end{align} $
Banyaknya persegi pada bangun datar (diagram kartesius) di bawah ini adalah ...
$ \begin{align} & (A). 8 \\ & (B). 10 \\ & (C). 12 \\ & (D). 14 \\ & (E). 20 \end{align} $
Soal No.16
Untuk setiap bilangan bulat $x$, $y$, $b$, $c$, $t$ dan $u$ didefinisikan
$\Bigg \langle \begin{matrix} x & t & b \\ & y & \\ u & c & \\ \end{matrix} \Bigg \rangle = (u \times c \times x)-((t \times u)-u) \times (b-y)$
Jika $a$ merupakan suatu bilangan prima dan genap.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
HTML Table Generator
Untuk setiap bilangan bulat $x$, $y$, $b$, $c$, $t$ dan $u$ didefinisikan
$\Bigg \langle \begin{matrix} x & t & b \\ & y & \\ u & c & \\ \end{matrix} \Bigg \rangle = (u \times c \times x)-((t \times u)-u) \times (b-y)$
Jika $a$ merupakan suatu bilangan prima dan genap.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
| $\Bigg \langle \begin{matrix} 3 & 7 & 5 \\ & 6 & \\ a & 2 & \\ \end{matrix} \Bigg \rangle$ | $25$ |
- Kuantitas $P$ lebih dari $Q$.
- Kuantitas $P$ kurang dari $Q$.
- Kuantitas $P$ sama dengan $Q$.
- Tidak dapat ditentukan hubungan kuantitas $P$ dan $Q$.
$a$ bilangan prima dan genap, artinya nilai $a$ pastinya $a=2$.
Sehingga,
$ \begin{align} & \Bigg \langle \begin{matrix} 3 & 7 & 5 \\ & 6 & \\ a & 2 & \\ \end{matrix} \Bigg \rangle = \Bigg \langle \begin{matrix} 3 & 7 & 5 \\ & 6 & \\ 2 & 2 & \\ \end{matrix} \Bigg \rangle \\ \\ &= (u \times c \times x)-((t \times u)-u) \times (b-y) \\ &= (2 \times 2 \times 3)-((7 \times 2)-2) \times (5-6) \\ &= 12-12 \times (-1) \\ &= 12+12=24 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah Kuantitas $P$ kurang dari $Q$.
Sehingga,
$ \begin{align} & \Bigg \langle \begin{matrix} 3 & 7 & 5 \\ & 6 & \\ a & 2 & \\ \end{matrix} \Bigg \rangle = \Bigg \langle \begin{matrix} 3 & 7 & 5 \\ & 6 & \\ 2 & 2 & \\ \end{matrix} \Bigg \rangle \\ \\ &= (u \times c \times x)-((t \times u)-u) \times (b-y) \\ &= (2 \times 2 \times 3)-((7 \times 2)-2) \times (5-6) \\ &= 12-12 \times (-1) \\ &= 12+12=24 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah Kuantitas $P$ kurang dari $Q$.
Soal No.17
Grafik fungsi $f(x)=3x^2+7x+1$ dan $g(x)=2x^2+5x+9$ berpotongan di dua titik berbeda, yaitu $P(m,n)$ dan $Q(k,l)$. Jika $m \gt k$ maka nilai dari $l-10m=$ ...
$ \begin{align} & (A). 5 \\ & (B). 4 \\ & (C). 3 \\ & (D). 2 \\ & (E). 1 \end{align} $
Grafik fungsi $f(x)=3x^2+7x+1$ dan $g(x)=2x^2+5x+9$ berpotongan di dua titik berbeda, yaitu $P(m,n)$ dan $Q(k,l)$. Jika $m \gt k$ maka nilai dari $l-10m=$ ...
$ \begin{align} & (A). 5 \\ & (B). 4 \\ & (C). 3 \\ & (D). 2 \\ & (E). 1 \end{align} $
Titik potong kedua kurva,
$ \begin{align} f(x) &= g(x) \\ 3x^2+7x+1 &= 2x^2+5x+9 \\ x^2+2x-8 &= 0 \\ (x+4)(x-2) &= 0 \\ x=-4 \ \text{atau} \ x&=2 \end{align} $
Karena $m \gt k$ maka kita dapatkan nilai $m=2$ dan $k=-4$.
Sehingga,
$ \begin{align} m=2 \to n &= 2(2)^2+5(2)+9 \\ &= 27 \\ \\ k=-4 \to l &= 2(-4)^2+5(-4)+9 \\ &= 21 \end{align} $
Dengan demikian, $l-10m= 21-10(2)=1$.
Jadi, pilihan jawaban yang TEPAT adalah $(E). 1$.
$ \begin{align} f(x) &= g(x) \\ 3x^2+7x+1 &= 2x^2+5x+9 \\ x^2+2x-8 &= 0 \\ (x+4)(x-2) &= 0 \\ x=-4 \ \text{atau} \ x&=2 \end{align} $
Karena $m \gt k$ maka kita dapatkan nilai $m=2$ dan $k=-4$.
Sehingga,
$ \begin{align} m=2 \to n &= 2(2)^2+5(2)+9 \\ &= 27 \\ \\ k=-4 \to l &= 2(-4)^2+5(-4)+9 \\ &= 21 \end{align} $
Dengan demikian, $l-10m= 21-10(2)=1$.
Jadi, pilihan jawaban yang TEPAT adalah $(E). 1$.
Soal No.18
Grafik fungsi $g(x)=x^2-20$ dan garis $ax-2y+30=0$ berpotongan di dua titik berbeda, yaitu $C(p,q)$ dan $D(-5,t)$. Garis $k$ melalui kedua titik tersebut. Nilai $a$ sama dengan ...
$ \begin{align} & (A). -5 \\ & (B). -4 \\ & (C). 4 \\ & (D). 5 \\ & (E). 7 \end{align} $
Grafik fungsi $g(x)=x^2-20$ dan garis $ax-2y+30=0$ berpotongan di dua titik berbeda, yaitu $C(p,q)$ dan $D(-5,t)$. Garis $k$ melalui kedua titik tersebut. Nilai $a$ sama dengan ...
$ \begin{align} & (A). -5 \\ & (B). -4 \\ & (C). 4 \\ & (D). 5 \\ & (E). 7 \end{align} $
$
\begin{align}
y &= x^2-20 \ \text{|} \times 2 \\
2y &= 2x^2-40 \\ \\
ax & -2y+30=0 \\
2y &= ax+30 \\ \\
2x^2-40 &= ax+30 \\
2x^2-ax-70 &= 0
\end{align}
$
Selanjutnya kita bisa pakai operasi akar pada persamaan kuadratnya untuk mencari nilai $a$ nya.
$ \begin{align} 2x^2 & -ax-70 = 0 \\ x_1 \cdot x_2 &= - \dfrac{70}{2} \\ p \cdot (-5) &= -35 \\ p &= 7 \\ \\ x_1 + x_2 &= - \dfrac{ \left(-a \right) }{2} \\ 7+(-5) &= \dfrac{a}{2} \\ a &= 4 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). 4$.
Selanjutnya kita bisa pakai operasi akar pada persamaan kuadratnya untuk mencari nilai $a$ nya.
$ \begin{align} 2x^2 & -ax-70 = 0 \\ x_1 \cdot x_2 &= - \dfrac{70}{2} \\ p \cdot (-5) &= -35 \\ p &= 7 \\ \\ x_1 + x_2 &= - \dfrac{ \left(-a \right) }{2} \\ 7+(-5) &= \dfrac{a}{2} \\ a &= 4 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). 4$.
Soal No.19
Sebuah sistem persamaan linier tiga variabel seperti nampak di bawah ini:
$4x-3y-z=1$
$2x+5y=-4$
$2x+5y+2z=4$
mempunyai solusi $a$, $b$, dan $c$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
HTML Table Generator
Sebuah sistem persamaan linier tiga variabel seperti nampak di bawah ini:
$4x-3y-z=1$
$2x+5y=-4$
$2x+5y+2z=4$
mempunyai solusi $a$, $b$, dan $c$.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas $P$ dan $Q$ berikut yang BENAR?
| $c^2-(4a^2+b^2)$ | $13$ |
- Kuantitas $P$ lebih dari $Q$.
- Kuantitas $P$ kurang dari $Q$.
- Kuantitas $P$ sama dengan $Q$.
- Tidak dapat ditentukan hubungan kuantitas $P$ dan $Q$.
Substitusikan persamaan kedua ke persamaan ketiga.
$ \begin{align} 2x+5y+2z &=4 \\ -4 +2z &= 4 \\ z &= 4 \\ \\ \end{align} $
Lanjut substitusikan nilai $z=4$ ke persamaan pertama dan eliminasi dengan persamaan kedua untuk mencari nilai $x$ dan $y$ nya.
$ \begin{align} 4x-3y-z &= 1 \\ 4x-3y-4 &= 1 \\ 4x-3y &= 5 \\ \end{align} $
$ \begin{array}{cc} 4x-3y &= 5 & \\ 4x+10y &= -8 & (-) \\ \hline -13y&=13 \\ y &= -1 \end{array} $
$ \begin{align} 4x-3(-1) &= 5 \\ 4x &= 2 \\ x &= \dfrac{1}{2} \end{align} $
Karena $x=a$, $y=b$ dan $z=c$ maka,
$ \begin{align} c^2-(4a^2+b^2) &= 4^2 - \left( 4 \left(\dfrac{1}{2} \right)^2 + (-1)^2\right) \\ &= 16 - 2 \\ &= 14 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah Kuantitas $P$ lebih dari $Q$.
$ \begin{align} 2x+5y+2z &=4 \\ -4 +2z &= 4 \\ z &= 4 \\ \\ \end{align} $
Lanjut substitusikan nilai $z=4$ ke persamaan pertama dan eliminasi dengan persamaan kedua untuk mencari nilai $x$ dan $y$ nya.
$ \begin{align} 4x-3y-z &= 1 \\ 4x-3y-4 &= 1 \\ 4x-3y &= 5 \\ \end{align} $
$ \begin{array}{cc} 4x-3y &= 5 & \\ 4x+10y &= -8 & (-) \\ \hline -13y&=13 \\ y &= -1 \end{array} $
$ \begin{align} 4x-3(-1) &= 5 \\ 4x &= 2 \\ x &= \dfrac{1}{2} \end{align} $
Karena $x=a$, $y=b$ dan $z=c$ maka,
$ \begin{align} c^2-(4a^2+b^2) &= 4^2 - \left( 4 \left(\dfrac{1}{2} \right)^2 + (-1)^2\right) \\ &= 16 - 2 \\ &= 14 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah Kuantitas $P$ lebih dari $Q$.
Soal No.20
Sebuah trapesium $ABCD$ dengan $AC$ sejajar $BD$, $A(2,1)$, $B(2,6)$, $C(5,1)$ dan $D(4,6)$ seperti tampak pada gambar di bawah ini.
Perbandingan luas segitiga $ABD$ dengan $ABCD$ adalah ...
$ \begin{align} & (A). 1:4 \\ & (B). 1:3 \\ & (C). 3:4 \\ & (D). 2:5 \\ & (E). 2:7 \end{align} $
Sebuah trapesium $ABCD$ dengan $AC$ sejajar $BD$, $A(2,1)$, $B(2,6)$, $C(5,1)$ dan $D(4,6)$ seperti tampak pada gambar di bawah ini.
Perbandingan luas segitiga $ABD$ dengan $ABCD$ adalah ...
$ \begin{align} & (A). 1:4 \\ & (B). 1:3 \\ & (C). 3:4 \\ & (D). 2:5 \\ & (E). 2:7 \end{align} $
Dari soal kita dapatkan,
Sehingga,
$ \begin{align} L_{ABD} &= \dfrac{1}{2} \times 2 \times 5 \\ &= 5 \ \text{satuan luas} \end{align} $
$ \begin{align} L_{ABCD} &= \left( \dfrac{2+3}{2} \right) \times 5 \\ &= \dfrac{25}{2} \ \text{satuan luas} \end{align} $
$ \begin{align} \dfrac{L_{ABD}}{L_{ABCD}} = \dfrac{5}{\frac{25}{2}} = \dfrac{2}{5} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 2:5$.
Sehingga,
$ \begin{align} L_{ABD} &= \dfrac{1}{2} \times 2 \times 5 \\ &= 5 \ \text{satuan luas} \end{align} $
$ \begin{align} L_{ABCD} &= \left( \dfrac{2+3}{2} \right) \times 5 \\ &= \dfrac{25}{2} \ \text{satuan luas} \end{align} $
$ \begin{align} \dfrac{L_{ABD}}{L_{ABCD}} = \dfrac{5}{\frac{25}{2}} = \dfrac{2}{5} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(D). 2:5$.
Penutup: UTBK Bukan Boss Terakhir, Tapi Wajib Ditaklukkan!
Gimana? Kita udah ngebedah bareng model soal Pengetahuan Kuantitatif UTBK SNBT 2025 dari awal sampai akhir.Rasanya kayak lagi main game level expert, tapi tenang ... setiap soal yang kamu kerjain itu bikin “level otak” naik terus.
Belajar UTBK tuh nggak harus tegang terus kayak nunggu ditembak sama dia hehe...
Santai, tapi serius. Capek boleh, nyerah jangan!
Ingat kata Goku di Dragon Ball Z,
"Power comes in response to a need, not a desire. You have to create that need."
Artinya? Kalau kamu ngerasa UTBK itu penting, otakmu bakal auto nyari cara buat ngerti, asal kamu mau mulai dulu.
Jadi, yuk terus belajar, latihan soal, dan jangan lupa jaga mental biar tetap waras. UTBK itu bukan boss terakhir hidup kamu, tapi tetep harus ditaklukin buat naik ke level selanjutnya.
Semangat, Pejuang SNBT 2026! Kalo karakter anime bisa ngeluarin jurus pamungkas pas kepepet, kamu juga bisa kok ngeluarin usaha maksimal pas ujian! 🎮📚🔥
"Kesuksesan nggak datang dari apa yang kamu lakukan sesekali. Tapi dari apa yang kamu lakukan secara konsisten." – Marie Forleo