Catatan Transformasi Fungsi Matematika Wajib Kelas 12 Kurikulum Merdeka
Ini adalah rangkuman lengkap materi tranformasi fungsi : tranlasi, refleksi, rotasi dan dilatasi kelas 12 matematika wajib kurikulum merdeka.
Materi ini sebenarnya bukan materi yang sebenarnya baru buat kamu yang sudah pakai kurikulum merdeka di sekolah saat kelas 11 nya.
Karena dasar - dasar dari transformasi geometri sudah kamu pelajari saat kelas 11.
Ngga jauh berbeda dengan transformasi geometri, hanya saja dikelas 12 materinya lebih mengerucut diperdalam pada fungsi yang ditransformasikan.
Oke.. gass kita bahas.
Transformasi ini dapat berupa pergeseran, pencerminan, rotasi, atau perubahan skala.
Jadi, berdasarkan jenisnya, transformasi fungsi tetap ada empat yang dipelajari yaitu :
Biar makin jelas lagi, kita bahas satu - satu ya. Tetap ikutin sampai habis.
dimana,
dimana,
Bayangan dari fungsi hasil transformasinya adalah :
dengan ketentuan nilai $a$ dan $b$ sama seperti di atas.
Ada dua jenis refleksi yang akan kita bahas kali ini yang bisa kamu perluas untuk jenis - jenis refleksi fungsi yang lain.
Dengan mengamati grafik refleksi vertikal terhadap sumbu-$X$ di bawah ini kamu akan paham bagaimana prinsip pencerminan diterapkan untuk mendapatkan sebuah fungsi bayangan hasil refleksinya.
Prinsip pencerminan secara horizontal dengan sumbu-$Y$ sebagai cerminnya diterapkan untuk mendapatkan sebuah fungsi bayangan hasil refleksinya terlihat pada gambar grafik di bawah ini.
Grafik $y = f(kx)$ adalah hasil dilatasi dari $y = f(x)$ dengan faktor $k$ yang sejajar sumbu-$X$.
Pada $y = f(kx)$ berlaku:
Grafik $y = kf(x)$ adalah hasil dilatasi dari $y = f(x)$ dengan faktor $k$ yang sejajar sumbu-$Y$.
Pada $y = kf(x)$ berlaku:
Karena faktor pengali ini merupakan faktor penentu letak dan ukuran grafik fungsi hasil dilatasi.
Hal yang harus kamu ingat adalah jika $\theta$ merupakan besar sudut rotasi (perputaran) maka:
Salah satunya adalah $90^{\circ}$ sama saja dengan $-270^{\circ}$.
Ada tiga jenis rotasi dasar yang harus kamu kuasai sebelum mempelajari rotasi dengan sudut - sudut yang lain.
Rotasi - rotasi ini adalah:
Mungkin awalnya kelihatan ribet, tapi makin dilatih, makin asyik, lho!
Ingat, matematika itu bukan soal siapa yang paling cepat, tapi siapa yang paling konsisten belajar.
Kalau kamu udah sampai di bagian ini, berarti kamu serius pengin paham.
Dan itu keren banget.
Jadi jangan berhenti sampai di sini ya!
Masih banyak materi seru dan catatan kece lainnya yang bisa bantu kamu makin jago matematika disini.
Ingat, kamu bukan cuma belajar buat ujian tapi juga buat masa depanmu yang cemerlang.
Jadi tetap semangat, terus eksplorasi, dan jadikan rasa penasaranmu sebagai bahan bakar belajar. Gas terus, pejuang SMA 12! 🚀📘
Materi ini sebenarnya bukan materi yang sebenarnya baru buat kamu yang sudah pakai kurikulum merdeka di sekolah saat kelas 11 nya.
Karena dasar - dasar dari transformasi geometri sudah kamu pelajari saat kelas 11.
Ngga jauh berbeda dengan transformasi geometri, hanya saja dikelas 12 materinya lebih mengerucut diperdalam pada fungsi yang ditransformasikan.
Oke.. gass kita bahas.
Apa itu Transformasi Fungsi
Transformasi fungsi adalah perubahan yang dilakukan pada suatu fungsi yang menghasilkan fungsi baru dengan grafik yang berbeda, tetapi masih berhubungan dengan fungsi aslinya.Transformasi ini dapat berupa pergeseran, pencerminan, rotasi, atau perubahan skala.
Jadi, berdasarkan jenisnya, transformasi fungsi tetap ada empat yang dipelajari yaitu :
- Translasi Fungsi (Pergeseran)
- Refleksi Fungsi (Pencerminan)
- Rotasi Fungsi (Perputaran)
- Dilatasi Fungsi (Pembesaran)
Biar makin jelas lagi, kita bahas satu - satu ya. Tetap ikutin sampai habis.
A. Translasi Fungsi
Translasi fungsi adalah transformasi yang memindahkan fungsi baik secara horizontal (searah sumbu-$X$) dan atau vertikal (searah sumbu-$Y$) pada jarak tertentu sehingga terbentuk sebuah fungsi baru yang merupakan bayangan hasil tranlasi fungsi semula.1. Translasi Horizontal
Jika kamu melakukan tranlasi horizontal pada sebuah fungsi $f(x)$ sejauh $a$ satuan maka fungsi bayangannya adalah :
$ y= f(x-a) $
dimana,
- $a \gt 0 \to$ fungsi bergeser ke kanan searah sumbu-$X$ positif.
- $a \lt 0 \to$ fungsi bergeser ke kiri searah sumbu-$X$ negatif.
2. Translasi Vertikal
Jika kamu melakukan tranlasi vertikal pada sebuah fungsi $f(x)$ sejauh $b$ satuan maka fungsi bayangannya adalah :
$ y= f(x)+b $
dimana,
- $b \gt 0 \to$ fungsi bergeser ke atas searah sumbu-$Y$ positif.
- $b \lt 0 \to$ fungsi bergeser ke bawah searah sumbu-$Y$ negatif.
3. Translasi Horizontal dan Vertikal
Kamu juga bisa melakukan translasi baik secara horizontal dan vertikal secara bersamaan.Bayangan dari fungsi hasil transformasinya adalah :
$ y= f(x-a)+b $
dengan ketentuan nilai $a$ dan $b$ sama seperti di atas.
B. Refleksi Fungsi
Refleksi fungsi adalah transformasi yang memindahkan sebuah fungsi berdasarkan sifat pencerminan terhadap garis sumbu (cermin) tertentu sehingga terbentuk sebuah fungsi baru yang merupakan bayangan hasil refleksi fungsi semula.Ada dua jenis refleksi yang akan kita bahas kali ini yang bisa kamu perluas untuk jenis - jenis refleksi fungsi yang lain.
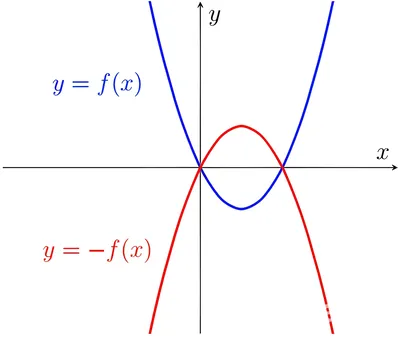
1. Refleksi Vertikal (Terhadap Sumbu-$X$)
Jika sebuah fungsi $f(x)$ direfleksikan (dicerminkan) secara vertikal dengan cermin sumbu-$X$ maka persamaan bayangannya adalah:
$ y= -f(x) $
Dengan mengamati grafik refleksi vertikal terhadap sumbu-$X$ di bawah ini kamu akan paham bagaimana prinsip pencerminan diterapkan untuk mendapatkan sebuah fungsi bayangan hasil refleksinya.
2. Refleksi Horizontal (Terhadap Sumbu-$Y$)
Jika sebuah fungsi $f(x)$ direfleksikan (dicerminkan) secara horizontal dengan cermin sumbu-$Y$ maka persamaan bayangannya adalah:
$ y= f(-x) $
Prinsip pencerminan secara horizontal dengan sumbu-$Y$ sebagai cerminnya diterapkan untuk mendapatkan sebuah fungsi bayangan hasil refleksinya terlihat pada gambar grafik di bawah ini.
C. Dilatasi Fungsi
Dilatasi fungsi adalah transformasi yang mengubah sebuah fungsi dengan faktor pengali ($k$) sehingga hasilnya merupakan pembesaran atau pengecilan grafik fungsi yang merupakan bayangan hasil dilatasi fungsi semula.1. Dilatasi Horizontal
Secara matematis jika kamu melakukan dilatasi horizontal pada sebuah fungsi $f(x)$ dengan faktor pengali $k$ satuan maka fungsi bayangannya adalah :
$ y= f(kx) $
Grafik $y = f(kx)$ adalah hasil dilatasi dari $y = f(x)$ dengan faktor $k$ yang sejajar sumbu-$X$.
Pada $y = f(kx)$ berlaku:
- Jika $k \gt 1$, maka grafik $y = f(kx)$ adalah grafik $y = f(x)$ yang diperkecil secara horizontal dengan membagi setiap koordinat $x$ dengan $k$.
- Jika $0 \lt k \lt 1$, maka grafik $y = f(x)$ adalah grafik $y = f(x)$ yang diperbesar secara horizontal dengan membagi setiap koordinat $x$ dengan $k$.
2. Dilatasi Vertikal
Dengan demikian juga jika kamu melakukan dilatasi vertikal pada sebuah fungsi $f(x)$ dengan faktor pengali $k$ satuan maka fungsi bayangannya adalah :
$ y= kf(x) $
Grafik $y = kf(x)$ adalah hasil dilatasi dari $y = f(x)$ dengan faktor $k$ yang sejajar sumbu-$Y$.
Pada $y = kf(x)$ berlaku:
- Jika $k \gt 1$, maka grafik $y = kf(x)$ adalah grafik $y = f(x)$ yang diperbesar secara vertikal dengan mengalikan setiap koordinat $y$ dengan $k$.
- Jika $0 \lt k \lt 1$, maka grafik $y = kf(x)$ adalah grafik $y = f(x)$ yang diperkecil secara vertikal dengan mengalikan setiap koordinat $y$ dengan $k$.
Karena faktor pengali ini merupakan faktor penentu letak dan ukuran grafik fungsi hasil dilatasi.
D. Rotasi Fungsi
Rotasi fungsi adalah transformasi yang memindahkan sebuah fungsi dengan cara memutar fungsi tersebut sejauh besaran sudut dan tumpuan (pusat) tertentu sehingga terbentuk sebuah fungsi baru yang merupakan bayangan hasil rotasi fungsi semula.Hal yang harus kamu ingat adalah jika $\theta$ merupakan besar sudut rotasi (perputaran) maka:
- $\theta$ positif jika diputar berlawanan arah jarum jam.
- $\theta$ negatif jika diputar searah arah jarum jam.
Salah satunya adalah $90^{\circ}$ sama saja dengan $-270^{\circ}$.
Ada tiga jenis rotasi dasar yang harus kamu kuasai sebelum mempelajari rotasi dengan sudut - sudut yang lain.
Rotasi - rotasi ini adalah:
- Rotasi $90^{\circ}$ atau $-270^{\circ}$.
- Rotasi $180^{\circ}$ atau $-180^{\circ}$.
- Rotasi $270^{\circ}$ atau $-90^{\circ}$.
\[ \begin{pmatrix}
x' \\
y'
\end{pmatrix} =
\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}
\begin{pmatrix}
x-a \\
y-b
\end{pmatrix} +
\begin{pmatrix}
a \\
b
\end{pmatrix}
\]
Contoh Soal dan Pembahasan Transformasi Fungsi
Beberapa contoh soal dan pembahasan berikut ini akan membantumu memahami lebih jauh bagaimana operasi matematika yang terjadi serta bagaimana cara mendapatkan fungsi bayangannya.
Soal No.1
Sebuah fungsi kuadrat $f(x)=2x^2-x+2$ ditranslasi $3$ satuan ke kanan searah sumbu-$X$ dan kebawah $1$ satuan searah sumbu-$Y$. Jika bayangan hasil translasi $f(x)$ adalah $f'(x)$ maka $f'(x)=$ ...
$ \begin{align} & (A). 2x^2-13x+22 \\ & (B). 2x^2+13x-22 \\ & (C). x^2-9x+12 \\ & (D). x^2-9x-12 \\ & (E). x^2-15x+21 \end{align} $
Sebuah fungsi kuadrat $f(x)=2x^2-x+2$ ditranslasi $3$ satuan ke kanan searah sumbu-$X$ dan kebawah $1$ satuan searah sumbu-$Y$. Jika bayangan hasil translasi $f(x)$ adalah $f'(x)$ maka $f'(x)=$ ...
$ \begin{align} & (A). 2x^2-13x+22 \\ & (B). 2x^2+13x-22 \\ & (C). x^2-9x+12 \\ & (D). x^2-9x-12 \\ & (E). x^2-15x+21 \end{align} $
$
\begin{align}
y &= f(x-a)+b \\
y &= f(x-3)+(-1) \\ \\
y &= 2(x-3)^2-(x-3)+2+(-1) \\
y &= 2(x^2-6x+9)-x+3+1 \\
y &= 2x^2-13x+22
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(A). 2x^2-13x+22$.
Jadi, pilihan jawaban yang TEPAT adalah $(A). 2x^2-13x+22$.
Soal No.2
Fungsi $f(x)=x^3+10x^2+3x+1$ ditranslasikan ke atas $3$ satuan searah sumbu-$Y$ maka bayangan dari $f(x)$ yang merupakan hasil dari translasi adalah ...
$ \begin{align} & (A). f(x)=3x^3+5x^2+3x+3 \\ & (B). f(x)=3x^3+8x^2+3x+5 \\ & (C). f(x)=x^3+10x^2+3x+4 \\ & (D). f(x)=2x^3-7x^2+6x \\ & (E). f(x)=2x^3+4x^2+3 \end{align} $
Fungsi $f(x)=x^3+10x^2+3x+1$ ditranslasikan ke atas $3$ satuan searah sumbu-$Y$ maka bayangan dari $f(x)$ yang merupakan hasil dari translasi adalah ...
$ \begin{align} & (A). f(x)=3x^3+5x^2+3x+3 \\ & (B). f(x)=3x^3+8x^2+3x+5 \\ & (C). f(x)=x^3+10x^2+3x+4 \\ & (D). f(x)=2x^3-7x^2+6x \\ & (E). f(x)=2x^3+4x^2+3 \end{align} $
Bayangan dari hasil translasi ke atas $3$ satuan ke atas adalah:
$ \begin{align} y &= f(x)+b \\ f(x) &=x^3+10x^2+3x+1 + 3 \\ f(x) &=x^3+10x^2+3x+4 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). f(x)=x^3+10x^2+3x+4$.
$ \begin{align} y &= f(x)+b \\ f(x) &=x^3+10x^2+3x+1 + 3 \\ f(x) &=x^3+10x^2+3x+4 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). f(x)=x^3+10x^2+3x+4$.
Soal No.3
Parabola $y=x^2+2x+5$ dicerminkan terhadap sumbu-$Y$, Persamaan bayangan parabola adalah ...
$ \begin{align} & (A). y=-x^2-2x+5 \\ & (B). y=-x^2+2x+5 \\ & (C). y=-x^2+2x-5 \\ & (D). y=x^2-2x-5 \\ & (E). y=x^2-2x+5 \end{align} $
Parabola $y=x^2+2x+5$ dicerminkan terhadap sumbu-$Y$, Persamaan bayangan parabola adalah ...
$ \begin{align} & (A). y=-x^2-2x+5 \\ & (B). y=-x^2+2x+5 \\ & (C). y=-x^2+2x-5 \\ & (D). y=x^2-2x-5 \\ & (E). y=x^2-2x+5 \end{align} $
Hasil pencerminan parabola $y=x^2+2x+5$ dicerminkan terhadap sumbu-$Y$ adalah:
$ \begin{align} y &= f(-x) \\ y &= (-x)^2+2(-x)+5 \\ y &= x^2-2x+5 \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E). y=x^2-2x+5 $.
$ \begin{align} y &= f(-x) \\ y &= (-x)^2+2(-x)+5 \\ y &= x^2-2x+5 \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(E). y=x^2-2x+5 $.
Soal No.4
Parabola $y=(x-4)^2-10$ dicerminkan terhadap sumbu-$X$, Persamaan bayangan parabola adalah ...
$ \begin{align} & (A). y=-x^2-8x+6 \\ & (B). y=-x^2+8x-6 \\ & (C). y=-x^2-8x-6 \\ & (D). y=x^2-8x+6 \\ & (E). y=x^2+8x+6 \end{align} $
Parabola $y=(x-4)^2-10$ dicerminkan terhadap sumbu-$X$, Persamaan bayangan parabola adalah ...
$ \begin{align} & (A). y=-x^2-8x+6 \\ & (B). y=-x^2+8x-6 \\ & (C). y=-x^2-8x-6 \\ & (D). y=x^2-8x+6 \\ & (E). y=x^2+8x+6 \end{align} $
Hasil pencerminan parabola $y=(x-4)^2-10$ dicerminkan terhadap sumbu-$X$ adalah:
$ \begin{align} y &= -f(x) \\ y &= -\left( (x-4)^2-10 \right) \\ y &= -\left( x^2-8x+6 \right) \\ y &= -x^2+8x-6 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). y=-x^2+8x-6$.
$ \begin{align} y &= -f(x) \\ y &= -\left( (x-4)^2-10 \right) \\ y &= -\left( x^2-8x+6 \right) \\ y &= -x^2+8x-6 \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). y=-x^2+8x-6$.
Soal No.5
Persamaan bayangan $y=x^2-10x$ oleh dilatasi pada pusat $O(0,0)$ dengan faktor skala $-\dfrac{1}{4}$ adalah ...
$ \begin{align} & (A). y=-\dfrac{1}{4}x^2-10x \\ & (B). y=-\dfrac{1}{16}x^2+\dfrac{5}{2}x \\ & (C). y=-4x^2-40x \\ & (D). y=-4x^2-10x \\ & (E). y=-4x^2-\dfrac{5}{2}x \end{align} $
Persamaan bayangan $y=x^2-10x$ oleh dilatasi pada pusat $O(0,0)$ dengan faktor skala $-\dfrac{1}{4}$ adalah ...
$ \begin{align} & (A). y=-\dfrac{1}{4}x^2-10x \\ & (B). y=-\dfrac{1}{16}x^2+\dfrac{5}{2}x \\ & (C). y=-4x^2-40x \\ & (D). y=-4x^2-10x \\ & (E). y=-4x^2-\dfrac{5}{2}x \end{align} $
Faktor skala $k=-\dfrac{1}{4}$, sehingga
$ \begin{align} y &= f(kx) \\ y &= f \left( -\dfrac{1}{4}x \right) \\ y &= \left( -\dfrac{1}{4}x \right)^2-10\left( -\dfrac{1}{4}x \right) \\ y &= -\dfrac{1}{16}x^2+\dfrac{10}{4}x \\ y &= -\dfrac{1}{16}x^2+\dfrac{5}{2}x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). y=-\dfrac{1}{16}x^2+\dfrac{5}{2}x$.
$ \begin{align} y &= f(kx) \\ y &= f \left( -\dfrac{1}{4}x \right) \\ y &= \left( -\dfrac{1}{4}x \right)^2-10\left( -\dfrac{1}{4}x \right) \\ y &= -\dfrac{1}{16}x^2+\dfrac{10}{4}x \\ y &= -\dfrac{1}{16}x^2+\dfrac{5}{2}x \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(B). y=-\dfrac{1}{16}x^2+\dfrac{5}{2}x$.
Soal No.6
Persamaan bayangan $y=x^3-1$ oleh dilatasi sejajar sumbu-$Y$ dengan skala $3$ adalah ...
$ \begin{align} & (A). y =3x^3-3 \\ & (B). y =3x^3+2 \\ & (C). y =27x^3-1 \\ & (D). y =27x^3-3 \\ & (E). y =x^3+2 \end{align} $
Persamaan bayangan $y=x^3-1$ oleh dilatasi sejajar sumbu-$Y$ dengan skala $3$ adalah ...
$ \begin{align} & (A). y =3x^3-3 \\ & (B). y =3x^3+2 \\ & (C). y =27x^3-1 \\ & (D). y =27x^3-3 \\ & (E). y =x^3+2 \end{align} $
Hasil persamaan bayangan $y=x^3-1$ oleh dilatasi sejajar sumbu-$X$ dengan skala $k=3$, yaitu:
$ \begin{align} y &=x^3-1 \\ \\ y &= f(kx) \\ y &= f(3x) \\ y &=(3x)^3-1 \\ y &=27x^3-1 \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). y =27x^3-1$.
$ \begin{align} y &=x^3-1 \\ \\ y &= f(kx) \\ y &= f(3x) \\ y &=(3x)^3-1 \\ y &=27x^3-1 \\ \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(C). y =27x^3-1$.
Soal No.7
Persamaan bayangan $y=4^x+10x$ oleh dilatasi sejajar sumbu-$Y$ dengan skala $2$ adalah ...
$ \begin{align} & (A). y =8^x+20x \\ & (B). y =8^x+10x \\ & (C). y =2^{2x}+10x \\ & (D). y =2^{2x}+20x \\ & (E). y =2^{2x+1}+20x \end{align} $
Persamaan bayangan $y=4^x+10x$ oleh dilatasi sejajar sumbu-$Y$ dengan skala $2$ adalah ...
$ \begin{align} & (A). y =8^x+20x \\ & (B). y =8^x+10x \\ & (C). y =2^{2x}+10x \\ & (D). y =2^{2x}+20x \\ & (E). y =2^{2x+1}+20x \end{align} $
$
\begin{align}
y &=4^x+10x \\ \\
y &= kf(x) \\
y &= 2f(x) \\
y &= 2(4^x+10x) \\
y &=2 \cdot 4^x+20x \\
y &=2 \cdot \left( 2^2 \right)^x+20x \\
y &=2^{2x+1}+20x \\
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(E). y =2^{2x+1}+20x$.
Jadi, pilihan jawaban yang TEPAT adalah $(E). y =2^{2x+1}+20x$.
Soal No.8
Persamaan grafik $y=3^{-x}+1$ setelah direfleksikan terhadap sumbu-$X$ adalah ...
$ \begin{align} & (A). y=3^x+1 \\ & (B). y=3^{-x}-1 \\ & (C). -y=3^{-x}+1 \\ & (D). y=\dfrac{1}{3^x}+1 \\ & (E). y=-\dfrac{1}{3^x}-1 \end{align} $
Persamaan grafik $y=3^{-x}+1$ setelah direfleksikan terhadap sumbu-$X$ adalah ...
$ \begin{align} & (A). y=3^x+1 \\ & (B). y=3^{-x}-1 \\ & (C). -y=3^{-x}+1 \\ & (D). y=\dfrac{1}{3^x}+1 \\ & (E). y=-\dfrac{1}{3^x}-1 \end{align} $
$
\begin{align}
y &= 3^{-x}+1 \\ \\
y &= -f(x) \\
y &= -\left( 3^{-x}+1 \right) \\
y &= - 3^{-x}-1 \\
y &= -\dfrac{1}{3^x}-1
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(E). y=-\dfrac{1}{3^x}-1 $.
Jadi, pilihan jawaban yang TEPAT adalah $(E). y=-\dfrac{1}{3^x}-1 $.
Soal No.9
Persamaan grafik $y=2^{x+1}-3$ setelah direfleksikan terhadap sumbu-$Y$ adalah ...
$ \begin{align} & (A). y = \dfrac{2^2}{2} -3 \\ & (B). y = \dfrac{2}{2^x} -3 \\ & (C). y = \dfrac{2^2}{2} +3 \\ & (D). y = \dfrac{2}{2^x} +3 \\ & (E). y = \dfrac{1}{2^x} - \dfrac{1}{3} \end{align} $
Persamaan grafik $y=2^{x+1}-3$ setelah direfleksikan terhadap sumbu-$Y$ adalah ...
$ \begin{align} & (A). y = \dfrac{2^2}{2} -3 \\ & (B). y = \dfrac{2}{2^x} -3 \\ & (C). y = \dfrac{2^2}{2} +3 \\ & (D). y = \dfrac{2}{2^x} +3 \\ & (E). y = \dfrac{1}{2^x} - \dfrac{1}{3} \end{align} $
$
\begin{align}
y &= 2^{x+1}-3 \\ \\
y &= f(-x) \\
y &= 2^{-x+1}-3 \\
y &= 2^{-x} \cdot 2^1 -3 \\
y &= \dfrac{1}{2^x} \cdot 2 -3 \\
y &= \dfrac{2}{2^x} -3 \\
\end{align}
$
Jadi, pilihan jawaban yang TEPAT adalah $(B). y = \dfrac{2}{2^x} -3$.
Jadi, pilihan jawaban yang TEPAT adalah $(B). y = \dfrac{2}{2^x} -3$.
Soal No.10
Jika $f'(x)$ merupakan persamaan bayangan kurva $f(x)=4x^2+1$ oleh rotasi $90^{\circ}$ terhadap pusat $O(0,0)$, maka $f'(x)=$ ...
$ \begin{align} & (A). \sqrt{\dfrac{-x-1}{4}} \\ & (B). \sqrt{\dfrac{x-1}{4}} \\ & (C). \sqrt{\dfrac{-x+1}{4}} \\ & (D). \sqrt{\dfrac{x+1}{4}} \\ & (E). \sqrt{\dfrac{-x+4}{2}} \end{align} $
Jika $f'(x)$ merupakan persamaan bayangan kurva $f(x)=4x^2+1$ oleh rotasi $90^{\circ}$ terhadap pusat $O(0,0)$, maka $f'(x)=$ ...
$ \begin{align} & (A). \sqrt{\dfrac{-x-1}{4}} \\ & (B). \sqrt{\dfrac{x-1}{4}} \\ & (C). \sqrt{\dfrac{-x+1}{4}} \\ & (D). \sqrt{\dfrac{x+1}{4}} \\ & (E). \sqrt{\dfrac{-x+4}{2}} \end{align} $
Untuk mencari persamaan bayangan kurvanya kita bisa peroleh dengan operasi matriks di bawah ini:
$ \begin{align} \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} \cos 90^{\circ} & -\sin 90^{\circ} \\ \sin 90^{\circ} & \cos 90^{\circ} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} -y \\ x \end{pmatrix} \\ \end{align} $
Sehingga kita peroleh $x=y'$ dan $y=-x'$, dengan demikian:
$ \begin{align} y &= 4x^2+1 \\ -x' &= 4(y')^2+1 \\ x' &= -4(y')^2-1 \\ x'+1 &= -4(y')^2 \\ \dfrac{x'+1}{-4} &= (y')^2 \\ \\ y &= \pm \sqrt{\dfrac{-x-1}{4}} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A). \sqrt{\dfrac{-x-1}{4}}$.
$ \begin{align} \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} \cos 90^{\circ} & -\sin 90^{\circ} \\ \sin 90^{\circ} & \cos 90^{\circ} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} -y \\ x \end{pmatrix} \\ \end{align} $
Sehingga kita peroleh $x=y'$ dan $y=-x'$, dengan demikian:
$ \begin{align} y &= 4x^2+1 \\ -x' &= 4(y')^2+1 \\ x' &= -4(y')^2-1 \\ x'+1 &= -4(y')^2 \\ \dfrac{x'+1}{-4} &= (y')^2 \\ \\ y &= \pm \sqrt{\dfrac{-x-1}{4}} \end{align} $
Jadi, pilihan jawaban yang TEPAT adalah $(A). \sqrt{\dfrac{-x-1}{4}}$.
Penutup: Yuk, Kuasai Transformasi Fungsi Bareng!
Nah, itu dia catatan seru tentang transformasi fungsi mulai dari fungsi yang digeser ke sana-sini, diperbesar atau diperkecil dan seterusnya.Mungkin awalnya kelihatan ribet, tapi makin dilatih, makin asyik, lho!
Ingat, matematika itu bukan soal siapa yang paling cepat, tapi siapa yang paling konsisten belajar.
Kalau kamu udah sampai di bagian ini, berarti kamu serius pengin paham.
Dan itu keren banget.
Jadi jangan berhenti sampai di sini ya!
Masih banyak materi seru dan catatan kece lainnya yang bisa bantu kamu makin jago matematika disini.
Ingat, kamu bukan cuma belajar buat ujian tapi juga buat masa depanmu yang cemerlang.
Jadi tetap semangat, terus eksplorasi, dan jadikan rasa penasaranmu sebagai bahan bakar belajar. Gas terus, pejuang SMA 12! 🚀📘
"Percaya bahwa kamu bisa adalah setengah dari perjalanan menuju keberhasilan." – Theodore Roosevelt